Questions:
Questions regarding vector spaces
1. Let u, x, y, z be elements in a vector space V where
u = 3x - 4y +5z, v = 4x + 5y - 6z, and 2u + 3v = x + y + z
Show that {x,y,z} is a linearly dependent set.
2. Find a basis for the space spanned by the following vectors
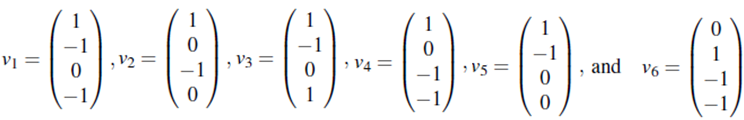
3. Let W = {p ∈P2 | p'(1) = 0}. That is, W are the functions in P2 whose derivative at 1 is 0. Show that W is a subspace of P2.
(a) Make a conjecture about the dimension of W. Explain your choice.
(b) Confirm (or reject) your conjecture by finding a basis for W.
4. Find a basis for the subspace V of R5 defined by the following equation
V = {(x1,x2,x3,x4,x5)∈R5}|x1 = 3x2 and x3 = 7x4
5. Find a basis for 2 x 2 matrices that includes [ 0 1; 1 1], [ -1 0: 0 1], and [ 0 0; 1 0] or explain why this is not possible.
6. Without any calculation, explain whether the following statements are true or false.
(a) We can add one vector to the set (3, 5, 2), (-3, 1, 2) to make a bsis for R3.
(b) A basis for R3 is the set {(2,3,1), (2,4,1), (4,6,5), (3,4,2)}
(c) A basis for R3 is the set {(12,-3,10), (0,14,9), (0,0,5)}
(d) A basis for P2 is {37x2 - 7x + 88,28x - 1,101}