question 1a the x and y components of fluid

Question

Question 1

(a) The x and y components of fluid velocity in a two-dimensional flow field are u=x and v= -y respectively

(i) Determine the stream function and plot the streamlines ψ=1 and 2

(ii) If a uniformed flow defined by ψ=y is superimposed on the above flow, determine the stream function and the velocity potential for this combined flow.

(b)  Explain the meaning of:

i) vorticity

ii) irrotational flow

iii) streamline

iv) stream function

v) velocity potential

Question 2

(a)  Air with a free stream velocity of 40 ms^-1 flows past a smooth plate which is 3 m wide and 10 m long in the flow direction. Assuming that air density is equal to 1.2 kg m^-3 and kinematic viscosity is equal to 1.49 10^-5 m²s^-1, determine

(i) The shear stress acting by the flow on the plate 6 m from the leading edge

(ii) The laminar sublayer thickness 6 m from the leading edge

(iii) The boundary layer thickness 6 m from the leading edge

(b) Explain the meaning of:

i) Reynolds stress tensor                                                                                                            

ii) Reynolds stress model

iii) averaged value                                                                                                         

iv) turbulent kinetic energy

Question 3

(a) All engineering CFD codes are focused on the solution of the following general equation

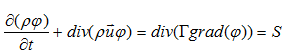
Simplify this equation assuming that all parameters change in one direction only, do not explicitly depend on time and assume that the source term is equal to zero

(b) Discretise the expression for the second derivative using the finite difference approach

(c) Discretise the following equation using the finite volume approach

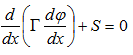
Question 4

The steady one-dimensional convection and diffusion equation can be presented in the form:

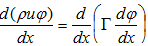
a) Discretise this equation using the central differencing finite volume approach

b) Discretise this equation using the upwind finite volume approach assuming that u is negative

c) Describe the range of applicability of the upwind approach

Question 5

(a)  An air stream with velocity 500 ms^-1, static pressure 60 kN m^-2 and temperature -18 °C undergoes a normal shock. Determine:

(i)  static pressure after the wave

(ii) stagnation pressure after the wave

(iii) air velocity after the wave

(NOTE: γ=1.4; R=287 J kg^-1 K^-1)

You may use the following relations without deriving it for the relations between Ma₁ and  Ma₂ and Ρ₁  and Ρ₂ 

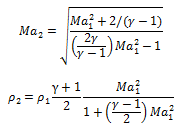
     (b)  Explain the meaning of:

       i) compressibility factor

       ii) continuity equation for normal shock waves

       iii) shock strength

Question 6

(a)  Starting with the Euler equation, derive the Bernoulli's equation for compressible flows

(b)  A venturi meter which has a throat diameter of 25 mm is installed in horizontal pipeline of 75 mm diameter conveying air. The absolute pressure at the inlet to the meter is 133.3 kPa and that at the throat is 100 kPa. Temperature of the air at the inlet 15 °C. Assuming isentropic flow determine the mass flow rate of air.