Proving set of all algebraic integers is countable

Question

(1) (a) Explain why Z X Z must be countable.

(b) By part (a) we know that N ≡ Z X Z, and hence there must be a one-to-one correspondence between N and Z X Z. Provide one such one-to-one correspondence f : N → Z X Z. Note, it may be easiest to explain your map using a sketch of Z X  Z.

(2) Proved in that a finite product of countable sets is countable. It is not true however that a countable product of count- able sets must be countable. Here you will see one example of a countable product of  finite sets that is not countable.

For each i ≡ N let A_i = {0,1} and let

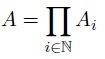
the set of all sequences of 1's and 0's. The set A is a countable product of  finite and hence countable sets. Prove that A is not countable.
(3) A complex number z is "algebraic" if it is a root of some integral polynomial (a polynomial with integer coefficients). That is z is algebraic if there is some

p(x) = a0 + a1x + a2x² +........+ a_kx^k a_i ≡ Z and at least one ai ≠ 0 with p(z) = 0. For example, the polynomial p(x) = -4+4x-x²+x³ factors to p(x) = (x- 1)(x - 2i)(x + 2i) and so has roots x = 1 and x = ± 2i, thus 1, 2i and -2i are algebraic numbers. Let A denote the set of all algebraic numbers in C, and prove that A is countable by the following steps.

(a) For each n ≡ N, let Pn denote the set of integral polynomials of degree n. Prove that for each n the set P_n is countable.

(b) Now let P be the set of all integral polynomials. Explain why P must be countable.

(c) Given a particular integral polynomial p(x) of degree k, let R_p be the set of all roots of p(x). What can be said about the number of elements in R_p?

(d) Using parts (a), (b) and (c), prove that A, the set of all algebraic integers, is countable.