Proving rouche theorem

Question

Question1) Z0 is removable if and only if limit from z to z0|f(z)| exists.

Question2) Calculate the integral: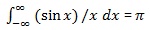

Question3) Prove 

1)

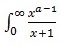         dx =π/(sin?(aπ))            ,0

2)

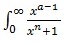  dx=π/(n  sin?(aπ)),0

Question4) Prove Rouche’s Theorem (original)

Suppose f,g are both analytic inside a simple closed contour c if ∀ z∈c, |f(z) |<|g(z) | then f,g have the same number of zeros inside contourc, counting multiplicities.

Question5)Prove that if f is a 1-1 analytic function in some domain, then f'(z)≠0 anywhere in D.

Question6)   Show that if f:R→R is such thatf' (x)≠0 ∀x∈R, then must be 1-1 function.

Question7) Show f:R²→R² given by f(x,y)=(e^x cosy,   e^x sin y) satisfies:
The Jacobian of f is nonsingular of all (x,y).
f is not 1-1.