Provides a measure of skewness in the distribution of x

Question

The continuous random variable X has probability density function (pdf) given by

                                           

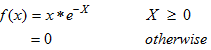
Show that, subject to t < 1, the Moment Generator Function, MGF, of X is:

                                                       

 

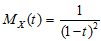
Use the series expansion method of the MGF to find E(X), E(X²) and E(X³), the first three moments of X about the origin. Use your results to show that the mean and variance of X are both equal to 2.

The standardised third moment, b₃ = E{ (X - m)³  ÷ s³  }, provides a measure of skewness in the distribution of X. Determine the value of b₃ for this distribution.  
                          
Using a suitable distributional approximation, find the probability that the mean of a random sample of n = 25 observations will exceed 2.5.