Prove the following statement using contraposition if n is

Question

1. Prove the following statement using the method of contradiction:

There are no positive integer solutions to the Diophantine equation x² - y² = 1.

2. Prove the following statement using contraposition: If n, is a positive integer such that n(mod 3) = 2, then n is not a perfect square.

3. Find a solution (if it exists) to the linear diophantine equation 234x + 65y = 325.

4. Prove that the sum to n terms of the sequence

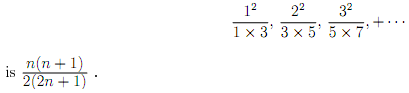
5. Prove using mathematical induction, that n³ - 7n + 3 is divisible by 3 for each integer n > 0.

6. The terms of a sequence are given recursively as

 

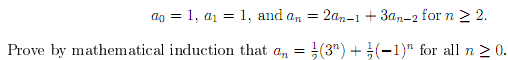
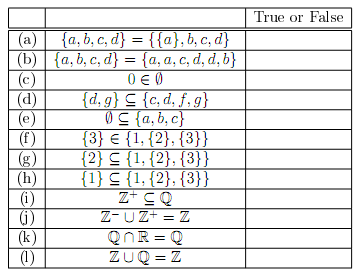
7. In each case decide whether the statement is true or false.