Properties of the determinant function

Question

Assignment:

Vectors in 2-Space and 3-Space : Properties of the determinant function

Q1. Verify that det(AB) = det(A) det(B) for

            A =   |2   1   0|        and       B =    |1   -1   3|

                    |3   4   0|                               |7    1   2|

                    |0   0   2|                               |5    0   1|

Is det(A+B) = det(A) + det(B) ?

Q2. Let A =    |a   b   c|

                      |d   e   f|

                      |g   h   i|

Assuming that det(A) = -7, find

b) det(A^-1)

e)  det       |a   g   d|

                  |b   h   e|

                  |c   i    f|

Q3. Prove the identity without evaluation the determinants.

      |a₁ + b₁|        |a₁ - b₁      c₁|                   |a₁    b₁    c₁|

      |a₂ + b₂|        |a₂ - b₂      c₂|   =    -2       |a₂    b₂    c₂|

      |a₃ + b₃|        |a₃ - b₃      c₃|                   |a₃    b₃    c₃|

Q4. Let A and B be n x n matrices.  Show that if A is invertible,

       then det(B) = det(A^-1BA)

Q5. Prove that a square matrix A is invertible if and only if A^TA is invertible.

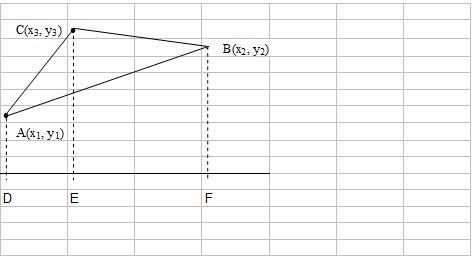
Q6. a) In the accompanying figure, the area of the triangle ABC can be expressed as

area ABC = ½    |x₁    y₁    1|

                          |x₂    y₂    1|

                          |x₃    y₃    1|

Note: In the derivation of this formula, the vertices are labeled such that the triangle is traced counterclockwise proceeding from (x₁, y₁) to (x₂, y₂) to (x₃, y₃).  For a clockwise orientation, the determinant above yields the negative of the area.

b)  Use the result in (a) to find the area of the triangle with vertices (3,3), (4,0), (-2, -1).

Figure

Euclidean Vector Spaces: Euclidean n-Space

Q1. Let u = (4, 1, 2, 3), v = (0, 3, 8, -2), and w = (3, 1, 2, 2).  Evaluate each expression.

a) ||u + v||    

b) ||u ||   +  || v ||

c) || -2u||   +  2 || u||

d) ||3u - 5v + w||

e) (1/||w||)w

f) ||1/ |w| w||

Q2. Find two vectors of norm 1 that are orthogonal to the tree vectors u = (2, 1, -4), v = (-1, -1, 2, 2), and w = (3, 2, 5, 4).

Q3. Find u · v given that ||u + v|| = 1 and  ||u - v||   = 5

Q4. Prove the following generalization of Theorem 4.1.7.  If v₁, v₂, ..., v_r are pairwise orthogonal vectors in Rⁿ, then

||v₁ + v₂ + ... + v_r ||² =   ||v₁||²  +  || v₂|| ²  + ... +   ||v_r||²

Q5. Use the Cauchy-Schwarz inequality to prove that for all real values of a, b, and q,

(a cosq + b sinq)²  ≤ a² + b²

Provide complete and step by step solution for the question and show calculations and use formulas.