Proof of cochrans theorem

Question

This homework assignment consists of five problems. Please show your work in detail, as answers with no justification.

1. Let Z _˜ N_p(0, I_P), and let A be a p x p matrix such that AA^T = V.

(a) Show that if Q is an orthogonal matrix, then QZ _˜ N_p(0, I_P)

(b) Show that (AQ)(AQ)^T = V.

(c) Show that X = μ + AQZ _˜ N_p(μ, V).

2. Let X _˜ N_p(μ, V) with V nonsingular, and let U = X^TAX for A symmetric.

(a) Show that the moment generating function for U is

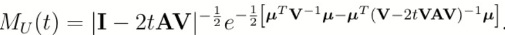
(b)    Show that if Aμ = 0, then

Mu(t) = |I — 2tAV|^-1/2

3. Using the result of Problem 2, show that

(a) Var(X^TAX) = 2tr(AV)² + 4μ^T(X^TAX)µ.

(b) If X _˜ N_p(0, V), then Var(X^TAX) = 2tr(AV)².

4. Prove the following Lemmas, with are related to the proof of Cochran's Theorem:

(a) Let A be a p x p symmetric matrix. Then A is idempotent if and only if rank(A) + rank(I — A) = p.

(b) If A, B, and A + B are all idempotent, then AB = 0.

(c) rank(_i=1Σ^k A_i) ≤ _i=1Σ^k rank(A_i).
 
5. In the normal linear model, i.e., Y _˜ N_p (Xβ, σ²I_N), find the conditional distribution of a^TY given X^TY. For simplicity, assume that X has full-column rank.