Problem 1. Suppose Jane and Lee are running for an elected position and are busy campaigning. Prior to the election the two candidates will debate several times and each candidate is considering what strategy they plan to take when their positions are questioned. One strategy is to respond with an aggressive rebuttal that defends the position that the candidate holds while a second strategy is to redirect the conversation and debate toward a new topic without addressing the issue. Both candidates have done research on the impact of these two strategies on likely voting outcomes and this is what they find. If Jane takes the aggressive rebuttal strategy while Lee simultaneously adheres to the same strategy, Jane sees her votes increase by 10 votes while Lee sees her votes increase by 8 votes. If Jane adheres to the redirect strategy while Lee adheres to the aggressive rebuttal strategy, Jane sees her votes increase by 6 votes while Lee sees her votes increase by 6 votes. If Jane adheres to the aggressive strategy while Lee adheres to the redirect strategy, Jane sees her votes increase by 7 votes while Lee sees her votes increase by 5 votes. If both candidates adhere to the redirect strategy, then both candidates see their votes increase by 5 votes each.
a) Given the above information fill in the following payoff matrix where each entry indicates the number of points won (a positive numeric value) or points lost (a negative numeric value)
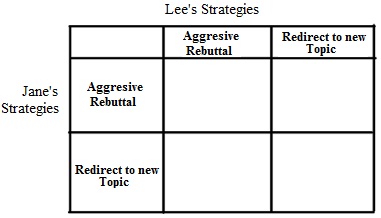
b) Examine the payoff matrix you created in (a). Does Jane have a dominant strategy? Explain your answer.
c) Examine the payoff matrix you created in (a).
Does Lee have a dominant strategy? Explain your answer.
d) Suppose Jane follows her dominant strategy, can you predict what Lee will do given the above information? Explain your answer.
e) You plan to watch Jane and Lee debateeach other this weekend. Describethe debate you anticipate seeing.
Who do you predict will win the election given this analysis?
Problem 2. Consider two firms in an industry consisting solely of these two firms. Lane Products and Forsyth Products produce identical products. Both firms are trying to decide whether they want to offer coupons or not offer coupons. They know that when they offer coupons the other firm is hurt by this policysince they are selling identical products. Lane Productsknows that if Forsyth Products offers coupons then Lane Products will earn a profit of $200,000 for the year if it also offers coupons and a profit of $80,000 for the year if it does not offer coupons. Lane Products knows that if Forsyth Products does not offer coupons then Lane Products will earn a profit of $120,000 for the year if it offers coupons and a profit of $100,000 for the year if it does not offer coupons.
Forsyth Products knows that if Lane Products offers coupons then Forsyth Products will earn a profit of $80,000 for the year if it also offers coupons and a profit of $60,000 for the year if it does not offer coupons. Forsyth Products knows that if Lane Products does not offer coupons then Forsyth Products will earn a profit of $100,000 for the year if it offers coupons and a profit of $60,000 for the year if it does not offer coupons.
a) Given the above information, construct a payoff matrix for this situation. Put Lane Products on the left hand side of the payoff matrix and Forsyth Products on the top of the matrix. Make sure your payoff matrix identifies the strategies that each firm faces as well as the payoff from each combination of strategies.
b) Identify if these two firms have the dominant strategies and, if so, what these dominant strategies are. Explain your answer.
c) Given the above information, can you predict what these two firms will do? Explain your answer.
Problem 3. Suppose there are two firms in a market and these two firms agree to form a cartel and divide up the market evenly. The two firms know the following:
Market Demand for the Product: P = 1000 – 2Q
Marginal Cost of producing the good: MC = 200
Fixed Cost of production: FC = 0
a) What is the profit maximizing quantity and price for the cartel? Explain your answer and provide a graph of this market to illustrate your answer.
b) What are the industry profits given your answer in (a)? Show your work.
c) What is the level of production for each firm if both firms adhere to the cartel agreement?
What are the profits for each firm? Explain your answer.
d) Suppose one of the firms decides to cheat on the cartel agreement and sell the product for $580 per unit. How many units can this firm sell at this price and what will be its profits when it follows this pricing strategy? Assume that the other firm does not drop its
price and consumers know all prices, so the other firm sells zero units.
e) Suppose that one of the firms drops its price as described in (d), but now the other firm matches this price decrease. If the two firms continue to split the market evenly, what will the profit for each firm equal now that both firms are selling the good for $580 per unit? Explain your answer.
f) Make a payoff matrix for these two firms with each firm having a choice of charging the profit maximizing price (see (a)) or the “cheating on cartel” price of $580. Put Firm A on the left hand side of the payoff matrix and Firm B at the top of the matrix.
g) Does each firm have a dominant strategy? Explain your answer.
h) What do you predict will be the outcome of this game? Explain your answer.
i) If you apply the above logic many times to successively lower prices (e.g. $580, $560, ...), what will the price eventually be?
Problem 4. Joe, Barb, and Cam live in the same community (they are the only residents) and they are debating installing some lighthouses. Thankfully each of these individuals is willing to reveal their preferences and demand for lighthouses, but the community is still trying to decide how many lighthouses they should buy. Here is the relevant information that they have gathered:
Joe’s demand for lighthouses: Q = 10 –2P
Barb’s demand for lighthouses: Q = 40 – 4P
Cam’s demand for lighthouses: Q = 10 – P
Marginal social cost of a lighthouse: MSC = $18
a) Given the above information draw an illustration of these three demand curves plus the market demand curve for lighthouses. In your illustration provide four different graphs that are vertically stacked with the market demand curve the bottom graph in the stack. Make sure all your graphs are clearly and completely labeled. Describe verbally how you found the market demand curve.
b) Write the equation(s) for the market demand curve and provide a range or domain for any segments of the demand curve. Show how you found these equations.
c) What is the socially optimal amount of lighthouses for this community? Explain how you found your answer. How much will Joe pay per lighthouse? How much will Barbpay per lighthouse? How much will Campay per lighthouse?
Problem 5. Consider the market for college education in the economy of Grand ville. The market demand curve for a year of college education is given by P = 50,000 – 2Q where P is the price per year of college and Q is the quantity of students attending college per year. This market demand curve expresses the marginal private benefit of going to college but does not include the social benefits derived from this education. The market supply curve for a year of college education is given by P = 2Q. This market supply curve expresses the marginal social cost of going to college. The social benefit of going to college for a year is equal to $10,000 per year per student, in addition to the private benefit that goes to the student directly.
a) Given the above description is there a negative or positive externality in this market? Explain your answer.
b) Given the above description,is this a consumption or a production externality? Explain your answer.
c) What quantity of students will attend college this year and what price will they pay given the above information? Show your work.
d) Suppose that the described externality is internalized in this market. Write the new equations we will need in order to find the socially optimal amount of college education to provide this year. Explain how you got these equations.
e) What is the socially optimal amount of college education to provide this year given the above information?
What is the “right” (the one that corresponds to the socially optimal amount of the good) price for a year of college? Explain your answer.
f) What is the deadweight loss that occurs when the externality is not internalized in this market? Show your work.