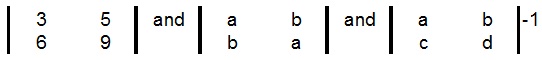Problems:
Questions:
Q1.Suppose An is the n by n tridiagonal matrix with 1's everywhere on the three diagonals:
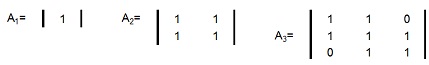
Let Dn be the determinant of An; we want to find it.
(a) Expand in cofactors along the first row of An to show that Dn = Dn-1 - Dn-2
(b) Starting from D1 = 1 and D2 = 0 find D3, D4, ..., D8. By noticing how these numbers cycle around (with what period?) find D1000.
Q2.Suppose the permutation S takes (1,2,3,4,5) to (5,4,3,2,1).
a) What does S2 do to (1,2,3,4,5)?
(b) What does S-1 do to (1,2,3,4,5)?
Q3.Find all the cofactors, and the inverse, of