Assignment:
Find , the constant force with the least magnitude that must be applied to the board in order to pull the board out from under the the box (which will then fall off of the opposite end of the board).
Express your answer in terms of some or all of the variables M1 ,M2 , Us ,g , and L.
Question 1. A window washer of mass M is sitting on a platform suspended by a system of cables and pulleys as shown . He is pulling on the cable with a force of magnitude F . The cables and pulleys are ideal (massless and frictionless), and the platform has negligible mass.
Find the magnitude of the minimum force that allows the window washer to move upward.
Express your answer in terms of the mass and the magnitude of the acceleration due to gravity .

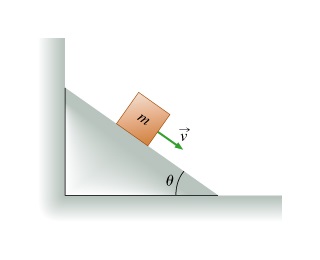
Question 2. Two blocks with masses M1 and M2 hang one under the other. For this problem, take the positive direction to be upward, and use g for the magnitude of the acceleration due to gravity.
a) Find T2, the tension in the lower rope.
Express your answer in terms of some or all of the variables M1, M2 ,and g.
B) Find T1, the tension in the lower rope.
Express your answer in terms of some or all of the variables M1, M2 ,and g.
C) Find T2, the tension in the lower rope.
Express your answer in terms of some or all of the variables M1, M2 ,a, and g.
D) Find T1 , the tension in the upper rope.
Express your answer in terms of some or all of the variables
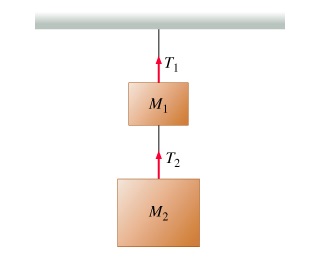
Question 3. A wedge with an inclination of angle rests next to a wall. A block of mass m is sliding down the plane, as shown. There is no friction between the wedge and the block or between the wedge and the horizontal surface.
A) Find the magnitude, Fnet , of the sum of all forces acting on the block.
Express Fnet in terms of Θ and ,m along with any necessary constants.
B) Find the magnitude, Fww , of the force that the wall exerts on the wedge.
Express in terms of Θ and , m along with any necessary constants