Assignment:
A Stereographic Projection
Consider a sphere of radius 1, with a plane inserted through the equator
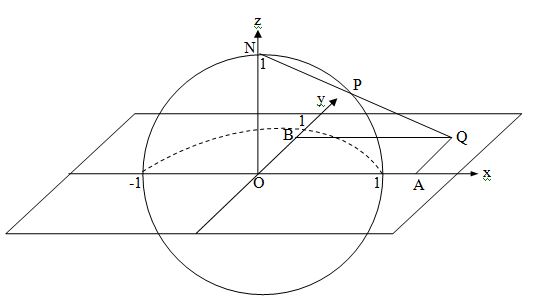
We map the sphere onto the plane by mapping a given point P onto Q, such that P, Q and the North Pole N all lie on the same line.
Show that circles on the sphere map to circles on the plane but if the circle on the sphere passes through the point N, it maps onto a line.
Provide complete and step by step solution for the question and show calculations and use formulas.