Assignment:
(1) Let (X, d) be a metric space, and f : X → X a continuous map. Prove that the function g : X → R defined by g(x) = d(x, f(x)) is a continuous function.
(2) Munkres 26.5
(3) Munkres 26.8
(4) Munkres 27.2
(5) Munkres 27.5
(6) For each of the following knots, use Seifert’s algorithm to draw a Seifert surface for each of the given knots. Make sure the two sides can be distinguished on your drawing (it helps to draw your diagram bigger). Use any of the techniques we saw on Thursday to find the genus of each surface.
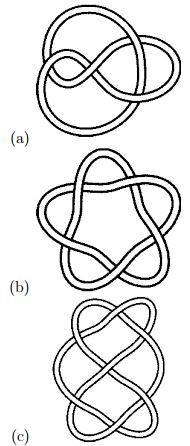
Note: the knots are drawn here as pieces of string, i.e., with some thickness, unlike how they may have been drawn in class.
Provide complete and step by step solution for the question and show calculations and use formulas.