Problem on linear regression model

Question

Simulate N = 10³ outcomes from the model

Y = -2 + X + ε

where X ~ U[0, 1] and ε ~ N(0, 0.1²) independently. From your simulated outcomes of (X, Y ), βt a linear regression model to increasing numbers of outcomes (from N = 2 to N = 10⁴) as y = β₀ + β₁x, by using the solution to the normal equations to obtain estimates for ^β = ( ^β₀, ^β₁)^T , via solving

(A^TA)β^ = A^Ty

where y = (y₁ , . . . , y_N)T , and

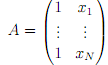
Plot your estimates for β₀ and β₁ as N increases, together with a line indicating their true values. Supply your code.