Problem based on mapping of matrix

Question

Question 1: Define a relation ∼ on R² by stating that (a, b) ∼ (c, d) if and only if a² + b² ≤ c² + d². Show that ∼ is reflexive and transitive but not symmetric.

- Reflexive

Let (a, b) ∈ R².

Then, a² + b² ≤ a² + b²

That is (a, b) ∼ (a, b)

Thus, ∼ is reflexive.

- Transitive

Let (a, b), (c, d), (e, f) ∈ R²

Suppose (a, b) ∼ (c, d) and (c, d) ∼ (e, f).

Then, a² + b² ≤ c² + d² and c² + d² ≤ e² + f²

That is a² + b² ≤ c² + d² ≤ e² + f²

In particular, a² + b² ≤ e² + f²

Then, (a, b) ∼ (e, f).

Thus, ∼ is transitive.

- Not Symmetric

Counterexample: Pick (1,1), (2,2) ∈ R²

(1,1) ∼ (2,2) is true since 1² + 1² ≤ 2² + 2²

but (2,2) ∼ (1,1) is false since 2² + 2² ? 1² + 1²

Question 2: Show that an m x n matrix give rise to a well-defined map from Rⁿ to R^m

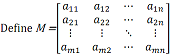
We can define a mapping: Rⁿ → R^m

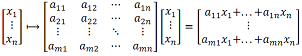
Question 3: Find the error in the following argument by providing a counterexample. "The reflexive property is redundant to the axioms for an equivalence relation. If x ∼ y, then y ∼ x by the symmetric property. Using the transitive property, we can deduce that x ∼ x."

Let R be the relation on the set A = {a, b, c} defined by R = {(a, a), (b, b), (a, b), (b, a)}

This is not an equivalence relation because it is not reflexive ((c, c) ∉ R) even though R is symmetric and transitive.

Since c is not related to some element say x ∈ A satisfying (c, x) ∈ R. Then, we are not allowed to use the argument cRx, xRc ⇒ cRc; since x does not exist.

Let σ = (1 3 5 7) and τ = (2 7 3) be elements of S₇

a) Find all elements of the subgroups <σ> and <τ>.

b) What order does σ have? What order does τ have? Can you generalize this to a statement for any cycle? σ is order 4 while τ because orders of permutations are determined by least common multiple of the lengths of the cycles.

c) Compute the product στ. What is its order?

στ = (1 2 7)(3 5), order 6.

Looking for a reliable and trustworthy Mapping of Matrix Assignment Help service in the industry?  Congratulations! Now, you don't have to be anxious now.

Tags: Mapping of Matrix Assignment Help, Mapping of Matrix Homework Help, Mapping of Matrix Coursework, Mapping of Matrix Solved Assignments, Reflexive Matrix Assignment Help, Reflexive Matrix Homework Help, Reflexive Matrix Coursework, Transitive Matrix Assignment Help, Transitive Matrix Homework Help, Transitive Matrix Coursework