Problem 1:
A plane stress element is subjected to stress components
σx = 50 MPa, σy = -10 MPa, and "τxy = 40 MPa.
1) Draw the Mohr's circle for this stress state.
2) Deterrnine the principal stresses and the angle of the principal direction to the x-axis.
3) Determine the maximum shear stress.
Problem 2:
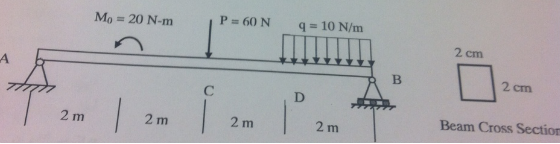
A simpie be beam subjected to a concentrated moment Mo, force P and a distributed load q
1) Determine the reaction forces at two ends (point A and B).
2) Draw the shear-force and bending moment diagram. Label values at all key points and the maximum. Label each section as constant, linear, quadratic, etc.
3) Determine the maximum shear stress τmax and maximum bending stress σmax in the cross-seaction, of the beam.
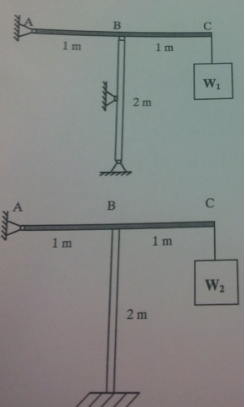
Problem 3:
A steel column (BD) is used to support a RIGID beam AC(length = 2m)that holds an object weight W. The steel column (E = 200GPa) has a square cross section of 40 mm x 400 mm length of L = 2m
Design 1(top): the column is pinned to the beam and the ground with an additional pinng at the middle.
Design II (bottom): the column is fixed at both ends
Deterrnine the buckling load (WI and W2) in "Design 1" and "Design 2". Which design can support larger load?
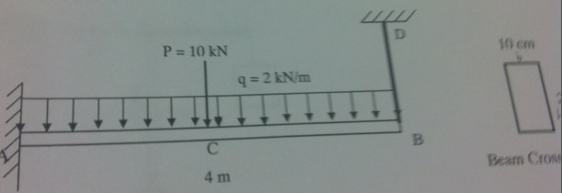
Problem 4:
A Steel cantilever beam AB is built in to the wall at me end A(fixed) and fixed and supported by a copper wire at end B. The beam is subjected to a concentrated force P=10 KN and a distributed force q = 2 KN/m
Steel Beam AB: Length L = 4 m with a rectangular cross section of hieght 20 cm x width 10 cm
Copper wire BD: Length h = 1m with a circular cross section of diameter d = 5mm
Is this system determinate or indeterminate?
Determine the deflection δB of the beam at the end B.
Problem 5:
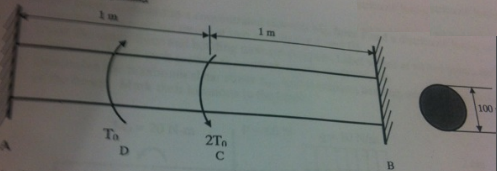
A circular shaft AB has a diameter of d =0.1 m. The total length of the bar is 2m. The shear modulus G = 90GPa
the shaft is fixed against rotation at both ends and subjected to TWO torques: To at point D) and 2T0 at the middle point C (see Figure). Torque To = 5 Kn -m
Determine the angle of rotation at the middle point C and reaction torque at end B.