1. A brewery produces two types of beer, stout and IPA. Each batch of stout sells for $60 per unit while every batch of IPA sells for $108. Both products need malt, barley, hops, filtered water, and yeast, measured in physical ‘units’ for convenience. Each batch of stout uses 1 unit of malt, 1 unit of hops, 2 units of barley, 5 units of yeast, and 10 units of filtered water. The corresponding requirements for IPA are: 5 units malt, 2 unit’s hops, 1 unit barley, 8 units yeast and nine unit’s water. On any given day, the brewery has on hand 150 units of malt, 90 units of hops, and 150 units of barley. The brewery pays $2 per unit for filtered water and $4 per unit of yeast.
a. Solve the problem graphically to find out the daily amounts of stout and IPA that maximize the brewer’s profits.
b. State and solve the dual problem by using the information you derived for primal problem.
c. Interpret dual problem in terms of the economics.
2. After some consultants point out that the Acme Toy Company has two bottlenecks in its manufacture of xylophones and yo-yos. The first is a critical grinding machine which only has 9 hours of capability per day. The second is warehouse space that is limited to 10 (thousand) square feet. Each production run of the xylophones needs 3 hours of grinding and take up two thousand square feet of storage while each yo-yo run needs one hour of grinding time and takes up 2000 square feet of storage. Each run of xylophones contributes $4 (thousand) to overhead and profit while each run of yo-yos contributes $2 (thousand).
a. Find out optimal amounts of each kind of toy to produce using graphical methods.
b. State and solve dual problem graphically.
c. Now solve the problem by using the revised simplex method. Do you get the same answers?
d. How much would the firm be ready to pay to raise the capacity of the grinding machine?
3. Consider the following simple economy which consists of two industries, guns (1) and butter (2) and is characterized by the following input-output matrix.
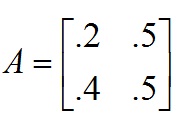
Assume also that the input-output vector of labor inputs is a = [.2 .4]. Assume consumers are expected to demand 10 units of guns and 20 units of butter. Also assume that the numeraire wage rate is w0=10.
a. Find out equilibrium quantities of guns and butter needed to satisfy consumer demand.
b. Find out the equilibrium prices to charge for each good.
c. Verify that economy is in equilibrium.
d. How many workers are employed?
e. Show that profits are 0 in all industries.
f. Are the Hawkins-Simon conditions satisfied? What would happen if they were not satisfied?
g. What would happen if the wage rate doubled?
4. Here is a snippet from military history. In the World War II Pacific Theatre Battle of the Bismarck Sea, the Japanese commander needed to send a convoy of ships from the eastern tip of New Guinea all the way around the island to the western port of Lae. He had his choice of sending the convoy around the island via the southern route (S) or the northern route (N). The southern route was shorter, but had better weather and therefore better visibility for possible bombing by Allied planes. The Allied commander had to choose where to send his planes.
If he concentrated on the southern route, and the Japanese commander chose to go that way, he could bomb for 3 days. If the Japanese commander chose the northern route he could only bomb for 1 day because of the bad weather. If the Allied commander chose to concentrate his planes on the northern route, he could bomb for 4 days if the Japanese commander went north because of the length of the trip, but he could bomb for only 2 days if the Japanese commander went south.
a. What should each commander do?
b. In fact the Japanese commander chose the northern route and so did the Allied commander, the result being a disaster for the Japanese.
Did the Japanese commander make a mistake? Was the Allied commander a genius?