Problem 1. Consider an aggregate production function
Q = 4 K1/2 L1/2 where Q is the number of widgets, K is the number of units of capital, and L is the number of units of labor. For this question assume K is initially fixed at 100 units. You also know that total cost,
TC, is given as TC = PkK + PlL
where Pk is the price of capital and Pl is the price of labor. Assume that the price of labor and the price of capital are both constant.
a) Fill in the missing cells of the table below based on the above information. (Hint: you might find it fun to do this with Excel: practice your spreadsheet skills and generate the numbers fa st!). Calculate your answers to two places past the decimal. Note: the numbers you get may not generate U - shaped curves
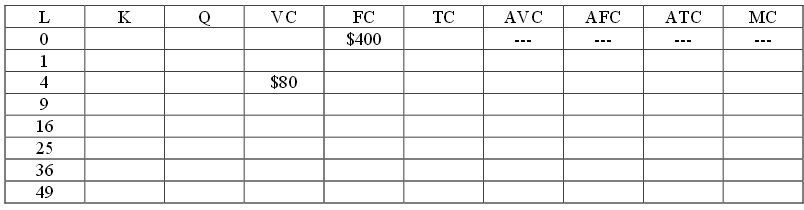
b) What is the price of capital? Explain how you got this answer.
c) What is the price of labor? Explain how you got this answer. d) Given the above information and your work in (a), fill in the following table. Round your answers to two places past the decimal. (Hint: if you used Excel earlier, you can continue to use Excel in this part of the exercise - just a great way to keep building your spreadsheet skills!)
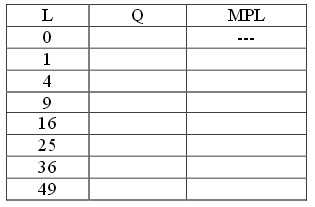
e) Given your work, does the production of this good show diminishing marginal returns to labor? Explain your answer.
f) Suppose that K doubles and L doubles. Without using numeric values, can you prove this production function has constant returns to sc ale? That is, can you show that if K and L both double that output, Q , will also double?
Question 2. Consider a perfectly competitive industr y composed of six identical firms that produce widgets . Suppose you are told that the representative firm has the following cost curves where TC is total cost measured in dollars and q is units of widgets produced by a particular firm :
Total Cost: TC = 4 + 4 q + q2
Marginal Cost: MC = 4 + 2q
Suppose you also know that the market demand curve is given by the following equation where P is the market price in dollars and Q is the market quantity of widgets :
Market Demand: P = 19 – (1/2)Q
Q represents market quantity and q represents firm quantity.
a) Given the above information write an equation for the market supply curve. Exp lain how you found this equation.
b) Given the market supply curve you found in (a), calculate the short run market equilibrium quantity and price in this market. How many units of output will the representative firm produce in the short run? Calculate t he short - run profits for the representative firm. Explain your work.
c) Given your calculations in (b), will the representative firm produce in the short - run? Explain your answer.
d) Given your answer in (b), what do you predict will happen in the long - run in this industry?
e) Given no changes in the firm’s cost curves or the market demand curve, calculate the following and explain how you found your answers:
Long - run equilibrium market price = ________
Long - run equilibrium market quantity = ________
Level of production by the representative firm = ________
Approximate number of firms in industry in the long - run (this will not be a whole number) = ________
Question 3. Consider a monopoly that produces widg ets . Suppose you are told that the monopoly has the following cost curves where TC is total cost measured in dollars, Q is the quantity of widgets, and P is the price per widget in dollars : Tot al Cost: TC = 4 + 4Q + Q2
Marginal Cost: MC = 4 + 2Q
Suppose you also know that the market demand curve is given by the following equation:
Market Demand: P = 19 – (1/2)Q
a) Given the above information, what is this monopolist’s equation for MR?
b) Determine the profit maximizing level of production for this monop olist as well as the price that will be charged for each unit of the good. Assume that this is a single price monopolist , i.e. the monopolist cannot engage in price discrimination . Explain how you found your answer.
c) Given the above information and you r answer in (b) calculate the level of profit in the short - run for this monopolist. Explain how you found your answer.
d) Given your answer in (c), what do you predict will happen to this monopolist in the long - run?
e) Calculate the deadweight loss that results from this market being served by a monopolist. Show how you found your answer. Provide a graph that is well labeled to illustrate your answer.
Question 4. Use the following graph of a natural monopolist to answer this next question. The graph depicts the market for a monopolist where LRATC is the long - run average total cost curve, MC is the marginal cost curve, and Demand is the market demand for the product. You are also told that the reciprocal of the slope of the market demand curve is -5
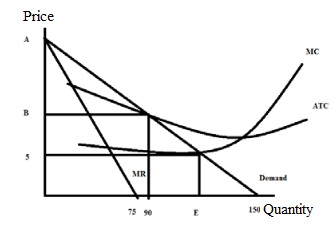
a) Given the above information and the graph, write the equation for the market demand curve in slope intercept form. Explain how you found your answer. You will need to provide a numeric value for “A” in the above graph.
b) Suppose that this monopolist is not regulated. Explain how this monopolist will determine its profit maximizing output and price. Assume that the monopolist is a single price monopolist. After explaining the process, identify the unregulated monopolist’s quantity and price on the grap h labeling the quantity (F) and the price (G). Note: you will not be able to actually compute F and G – just label them on a well - drawn diagram.
c) Will the monopolist described in (b) earn positive, negative, or zero economic profits? Explain your answer.
d) Suppose that this monopolist is regulated with a MC pricing regulation. This insures that the monopolist produces the socially optimal amount of the good, but will require a subsidy for the producer since economic profits will be negative. From the g raph and your prior work, identify (that is, provide a numeric value) the socially optimal amount of the good. Then amend the graph to show the amount of total subsidy this monopolist will need to receive if they are to produce the socially optimal amount of the good.
e) Suppose that this monopolist is regulated with AC pricing regulation. This insures that the monopolist produces the level of output where its economic profit is equal to zero. From the graph and your prior work, identify (that is, provide a numeric value) of the price the monopolist will charge if it is regulated to produce that level of output where the monopolist breaks even. Amend the graph to provide this numeric value.
Question 5. Consider a market that is served by a single producer. This market has significant barriers to entry so the single producer has market power and is not likely to face any competition due to these barriers of entry. You are given the following information about this market:
Market Demand: Q = 450 – 3P
MC = 30
Fixed Cost for the Producer: FC = 50
a) Given the above information, if this producer acts as a single price monopolist, calculate the following:
Profit maximizing quantity = ______
Profit maximizing price = _____
Level of profits = _______
Consumer Surplus = CS = ______
Producer Surplus (remember you will need to adjust this to take into account FC) = PS = ______
Deadweight Loss = _______
Show your work and provide a graph to illustrate your answer.
b) Suppose that this mon opolist decides to practice second degree price discrimination. The monopolist decide s that it will sell its first 90 units of the good produced for a price of $120 per unit , its next thirty units f or a price of $110 per unit, its ne xt sixty units for a price of $9 0 per unit , and a final thirty units for a price of $80 per unit.
Given this information and the initial information, calculate the following for the monopolist who practices this second degree price discrimination: Total quantity produced by th e second degree price discriminator = ______
Prices charged by the second degree price discriminator = _______
Level of profits for the second degree price discriminator = _______
Consumer Surplus in this case of second degree price discrimination = CS ’ = ______
Producer Surplus ( remember you will need to adjust this to take into account FC ) in this case of second degree price discrimination = PS ’ = _______
Deadweight Loss in this case of second degree price discrimination = _______
Show your work and provide a graph to illustrate your answer.
c) Compare your answers in (a) and (b). Does second degree price discrimination benefit consumers in this case ? Explain your answer here and provide evidence to support your answe r. Does second degree price discrimination benefit the producer? Explain your answer here and provide evidence to support your answer.
d) Suppose this monopolist is able to practice first degree price discrimination in this market. Compute the following if this monopolist successfully implements first degree price discrimination.
Total amount of the good produced in the market = ________
PS” with perfect price discrimination (remember to account for those fixed costs) = _____
CS” with per fect price discrimination = _______
Profit for firm with perfect price discrimination = ______
DWL with perfect price discrimination = _______
Show your work and provide a g raph to illustrate your answer.
Question 6. Karen is a supplier of dr y cleaning services in her small town. She operates the only dry cleaning service and therefore has significant market power. She knows that she has two types of clients: business clients who come in regularly to have their clothing cleaned and non - business clients who have occasional garments to clean. She knows the following information where Q is the quantity of dry cleaning units and P is the price per unit of dry cleaning :
Demand for dry cleaning services fr om business clients: Q = 20 – (1/2)P
Demand for dry cleaning services from non - bus iness clients: Q = 30 - P
MC of providing dry cleaning services: MC = 4
Fixed Costs of providing dry cleaning services: FC = 10
Suppose that Karen decides to treat her dry cleaning business as two separate monopolies: one providing dry cleaning services to business clients and one providing dry cleaning services to non - business clients. She can readily identify the status of each of her clients sinc e she has been in business in this small town for a long, long time and she knows her customers well.
a) Given that Karen is going to treat these two types of customers as separate entities, what will be the profit maximizing price and quantity of the go od for each type of customer? And, what 6 will total profits be equal to? Show how you found your answers to this set of questions clearly and logically! Provide a set of graphs to illustrate your answer.
b) Now, suppose Karen would like to verify that thi s two pricing scheme idea in (a) actually results in her earning greater profits than if she were to simply follow a single pricing monopoly model. So, find the market demand curve. Then determine the profit maximizing quantity and price if Karen treats th is market as a single market with one price for dry cleaning. What happens to the level of profits Karen earns under this pricing decision? Provide numeric values for all your work and clearly and logically explain how you found your answers. Also, provide a graph to illustrate your answer.