Problem 1: Price Discrimination
Consider a market served by a single producer. The total cost function for this monopolist is TC = 0.5Q2 .
The marginal cost function for the monopolist is MC = Q. Furthermore, suppose there are two classes of buyers in th is market. Demand for the respective classes is given by the following equations:
Class I: P = 10 – Q/2
Class II: P = 14 – 2Q
a. First suppose the government makes it illegal for the monopolist to sell to Class I consumers. In this case the monopolist’s market demand curve is P = 14 – 2Q, the demand curve of Class II. Suppose the monopolist is able to practice first-degree price discrimination when providing this good to Class II buyers.
(1) What is the price for the 5th unit purchased?
(2) Draw a graph of the demand curve and marginal cost curve (with price and MC on the vertical-axis and quantity on the horizontal-a xis) for this perfect price discriminating monopolist.
(3) Calculate the value of producer surplus. Shade the are a on your graph that corresponds to producer surplus and label this area clearly.
(4) Calculate the value of consumer surplus. Shade the area on your graph that corresponds to producer surplus and label this area clearly.
(5) Is this market allocatively efficient? Why or why not?
b. Now suppose the monopolist is allowed to sell to both classes but the monopolist CANNOT distinguish between the two classes.
(1) Find the equation for the combined market demand (this equation should be solved for Q as a function of P). Draw a new graph which shows the market demand and marginal cost. (Hint: you should have two e quations to express the demand curve for the monopolist.)
(2) What is the equation for marginal revenue when this m onopolist sells to both classes, but cannot distinguish between the two classes? Add the MR curve to your graph. (Hint: you should have two equations to express the MR curve for the monopolist.)
(3) Complete the following:
The quantity the monopolist produces: QM =
The monopolistic price: PM =
The quantity demanded by Class I: Q1 =
The quantity demanded by Class II: Q2 =
Consumer surplus for Class I: CSI =
Consumer surplus for Class II: CS II =
The monopolist’s profit: π =
(4) Draw two graphs: on the first graph represent Class I demand and on the second graph represent Class II demand. Shade the area that represents CS I on the first graph and the area that represents CS II on the second graph: label these areas clearly.
c. Now suppose that the monopolist can identify buyers from each class. Also assume that buyers from one class cannot resell the good to buyers from the other class. The monopolist will practice third-degree price discrimination by setting separate prices, P1 and P2 for Class I and Class II respectively.
(1) What is the marginal revenue equation for Class I (MR1)? Draw a graph which shows the demand and marginal revenue curves for Class I. Label these curves clearly.
(2) What is the marginal revenue equation for Class II (MR2)? Draw a graph which shows the demand and marginal revenue curves for Class II . Label these curves clearly.
(3) Complete the following:
The quantity sold to Class I: Q1 =
The quantity sold to Class II: Q2 =
The price charged to Class I: P1 =
The price charged to Class II: P2 =
Consumer surplus for Class I: CS I =
Consumer surplus for Class II: CS II =
The monopolist’s profit: π =
(4) Compare the results from parts b. and c. by completing the following sentences. The monopolist gains ________ (higher or lower) profit by 3rd degree price discrimination.
Class I consumers whose demand curve is more _________ (elastic or inelastic) have ________ (higher or lower) consumer surplus under 3rd degree price discrimination.
Class II consumers whose demand curve is more ___________ (elastic or inelastic) have _________ (higher or lower) consumer surplus with 3 rd degree price discrimination.
Problem 2: Factor Markets
The following table gives cost information for each firm in the digital camera industry. Assume that this industry is characterized by perfect compet ition in both the input and the output markets: that is, all firms in the digital camera industry are price-takers both in the factor (labor and capital) and product (digital camera) markets. Assume that capital is paid a constant price of $80 per unit. Suppose that in the long-run equilibrium the market price of a digital camera is $10. Assume that a ll firms in this industry are identical and face the same cost curves.
(1) Given the above information, what is the equation fo r marginal revenue (MR) for a representative firm in the long-run?
The market supply curve for labor is QL = PL , i.e., when the wage is PL , the total number of willing workers is: QL = PL . The market demand curve for labor is QL = 60 - PL , i.e., when the wage is PL, there is a total of (60- PL) workers hired by the digital camera firms.
(2) What is the equilibrium wage per unit of labor (PL)? In equilibrium how many workers (labor) are working in this industry (QL)? Use this information to complete the VC column in the table below.
Note: L is labor; K is capital; Q is output; TR is Tot al Revenue.
MPL = ?Q/ ?L = Marginal Product of Labor, i.e., the additional output generated by employing one more unit of labor.
MRP = ?TR/?L = (?TR/?Q)×(?Q/?L) = MR×MPL = value of the marginal product of labor (or VMPL ), i.e., the value of the additional ouput generated by employing one more unit of labor.
MC = ?TC/?Q = ?VC/?Q
MFC = ?TC/?L = Marginal Factor Cost (of labor) holding other factors constant.
(3) Complete the following table.
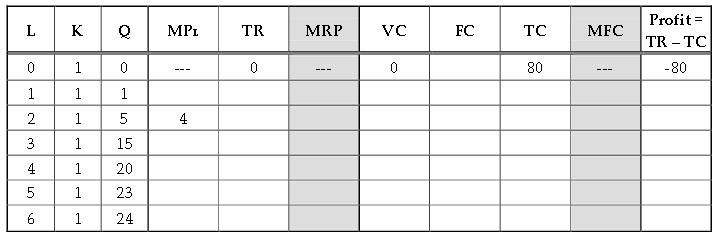
(4) How many units of labor will make MRP = MFC for a re presentative firm? Is the profit maximized at this level of labor usage? How m any units of labor will one firm hire?
(5) Now suppose the government makes it legal for firms to hire illegal immigrants. This results in a new market labor supply curve: QL = 40 + PL . The market demand curve for labor is not changed (QL = 60 - PL). What is the new equilibrium market wage per unit of labor? What is t he new MFC for a representative firm? Suppose the demand and supply cu rves for digital cameras are not changed in the short run, i.e., the market price of the digital camera is still $10. Without writing another table, do you know ho w many units of labor one firm will hire?
Problem 3: Monopolistic Competition
You are a member of an unnamed governmental intelli gence-service agency. You’ve been sent to Tangiers Morocco to investigate an industry of interest. This industry produces a good which we’ll call “the product”. Once in Tangiers you observe that the market for this product is monopolistically competitive . After a complicated series of events you are able to obtain some information about one firm in this monopolistically competitive industry. Specifically, you find that this firm:
faces demand: P = 350 – Q/2,
has total costs: TC = 10 + 50Q + Q2/4,
has marginal costs: MC = 50 + Q/2.
Before you can submit your initial report you need to answer some preliminary questions:
a. Derive the marginal revenue curve for this firm.
b. Draw the demand, MR and MC curves for this firm in one graph.
c. What is the optimal quantity for this firm to produ ce if the firm’s goal is to profit maximize?
d. Calculate the profit for this firm.
e. Predict what is going to happen in the long run to this firm and illustrate this long run outcome in a graph.
Problem 4: Game Theory Agent Sneaky and Agent Sly can each choose between two strategies. Each agent makes their choice of strategy at the same time (i.e. they cannot observe the other agent’s move before choosing their own move).

Each of the following matrices shows the strategies avai lable to each agent and the payoff from each strategy choice. The payoff is shown w ith payoff to Sly first, then payoff to Sneaky. Assume a larger number payoff is supe rior to a smaller number payoff.
a. Find the dominant strategy for each agent (if one exists).
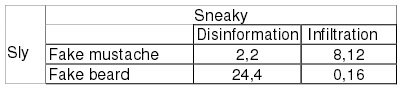
b. Find the dominant strategy for each agent (if one exists)
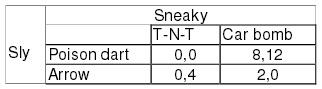
c. Find the dominant strategy for each agent. Whi ch agent ends up with the highest payoff?
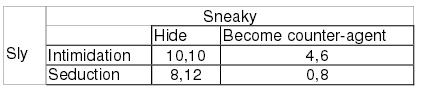
Problem 5:
Game Theory Jason Bourne has been hiding in an office building acro ss from C.I.A. headquarters for 32 hours. Bourne is starting to get very hungry and he is seriously considering ordering a pizza. If Bourne can order a pizza without being detected he gets 10 utils. If he doesn’t order the pizza he gets 0 utils.
Kevin Kislouski from Omaha Nebraska has a summer inter nship at the C.I.A.. His job is to monitor city phone lines for any sign of Jason Bourne . Kislouski has been listening for the past 6 hours and he really has to go to the bathroom.
If Bourne makes the call and Kislouski is listening the n Kislouski will be able to locate Bourne. This would cause Bourne’s utility to drop to - 10 but Kislouski would get 10 utils. If Kislouski leaves his post to go to the bathroom and misses Bourne’s call then Kislouski gets -10 utils but if Bourne doesn’t make a call while he’s gone then Kislouski gets 10 utils. If Kislouski decides not to take a bathroom br eak and Bourne doesn’t make a call then Kislouski gets 0 utils.
a. Set up the payoff matrix for this game with Bour ne’s choices represented on the left hand side of the matrix and Kislouski’s choices represente d across the top of the matrix.
b. Is Bourne better off ordering a pizza regardless o f Kislouski’s strategy choice?
c. Does Bourne have a dominant strategy?
d. Suppose Bourne is watching Kislouski from his hiding place across the street from C.I.A. headquarters. Now Bourne can make his strateg y choice contingent on Kislouski’s strategy choice. How will Bourne respond to either of Kislouski’s strategy options and what will the resulting payoff to Bourne and Kislouski be in each case?