Assignment:
Part I:
Q1. How is dividing a polynomial by a binomial similar to or different from the long division you learned in elementary school? Can understanding how to do one kind of division help you with understanding the other kind? What are some examples from real life in which you might use polynomial division?
Q2. How do you determine if a polynomial is the difference of two squares?
Q3. Take any number (except for 1). Square that number and then subtract one. Divide by one less than your original number. Now subtract your original number. Did you reached 1 for an answer? You should have. How does this number game work? (Hint: Redo the number game using a variable instead of an actual number and rewrite the problem as one rational expression). How did the number game use the skill of simplifying rational expressions? Create your own number game using the rules of algebra and post it first and then solve it. Be sure to think about values that may not work. State whether your number game uses the skill of simplifying rational expressions.
Q4. How is doing operations (adding, subtracting, multiplying, and dividing) with rational expressions similar to or different from doing operations with fractions? Can understanding how to work with one kind of problem help understand how to work another type? When might you use this skill in real life?
Q5. When solving a rational equation, why is it necessary to perform a check?
Q6. Why is it important to simplify radical expressions before adding or subtracting? How is adding radical expressions similar to adding polynomial expressions? How is it different? Provide a radical expression for the assignment to simplify.
Q7. What is the Pythagorean theorem? How is it used?
Q8. How do you know if a quadratic equation will have one, two, or no solutions? How do you find a quadratic equation if you are only given the solution? Is it possible to have different quadratic equations with the same solution? Explain. Provide your answer with one or two solutions with which they must create a quadratic equation.
Q9. Quadratic equations can be solved by graphing, using the quadratic formula, completing the square, and factoring. What are the pros and cons of each of these methods? When might each method be most appropriate? Which method do you prefer? Why?
Q10. If you are looking at a graph of a quadratic equation, how do you determine where the solutions are?
Part II:
Simplifying and Factoring Polynomials. Complete problem applied to a real-life situation.
Application Practice
Answer the following questions to the problem.
Q1. In this problem, we will analyze the profit found for sales of decorative tiles. A demand equation (sometimes called a demand curve) shows how much money people would pay for a product depending on how much of that product is available on the open market. Often, the demand equation is found empirically (through experiment, or market research).
a. Suppose that a market research company finds that at a price of p = $20, they would sell x = 42 tiles each month. If they lower the price to p = $10, then more people would purchase the tile, and they can expect to sell x = 52 tiles in a month’s time. Find the equation of the line for the demand equation. Write your answer in the form p = mx + b. (Hint: Write an equation using two points in the form (x,p)).
A company’s revenue is the amount of money that comes in from sales, before business costs are subtracted. For a single product, you can find the revenue by multiplying the quantity of the product sold, x, by the demand equation, p.
b. Substitute the result you found from part a into the equation R = xp to find the revenue equation. Provide your answer in simplified form.
The costs of doing business for a company can be found by adding fixed costs, such as rent, insurance, and wages, and variable costs, which are the costs to purchase the product you are selling. The portion of the company’s fixed costs allotted to this product is $300, and the supplier’s cost for a set of tile is $6 each. Let x represent the number of tile sets.
c. If b represents a fixed cost, what value would represent b?
d. Find the cost equation for the tile. Write your answer in the form C = mx + b.
The profit made from the sale of tiles is found by subtracting the costs from the revenue.
e. Find the Profit Equation by substituting your equations for R and C in the equation P= R - C . Simplify the equation.
f. What is the profit made from selling 20 tile sets per month?
g. What is the profit made from selling 25 tile sets each month?
h. What is the profit made from selling no tile sets each month? Interpret your answer.
i. Use trial and error to find the quantity of tile sets per month that yields the highest profit.
j. How much profit would you earn from the number you found in part i?
k. What price would you sell the tile sets at to realize this profit (hint, use the demand equation from part a)?
Q2. The break even values for a profit model are the values for which you earn $0 in profit. Use the equation you created in question one to solve P = 0, and find your break even values.
Q3. In 2002, Home Depot’s sales amounted to $58,200,000,000. In 2006, its sales were $90,800,000,000.
a. Write Home Depot’s 2002 sales and 2006 sales in scientific notation.
You can find the percent of growth in Home Depot’s sales from 2002 to 2006, follow these steps:
• Find the increase in sales from 2002 to 2006.
• Find what percent that increase is of the 2002 sales.
b. What was the percent growth in Home Depot’s sales from 2002 to 2006? Do all your work by using scientific notation.
(source: Home Depot Annual Report for FY 2006: https://www6.homedepot.com/annualreport/index.html)
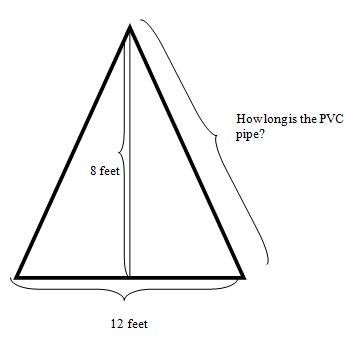
Q4. A customer wants to make a teepee in his backyard for his children. He plans to use lengths of PVC plumbing pipe for the supports on the teepee, and he wants the teepee to be 12 feet across and 8 feet tall (see figure). How long should the pieces of PVC plumbing pipe be?
Part III:
Application Practice
Answer the following questions.
The cost, in millions of dollars, to remove x % of pollution in a lake modeled by C = 6000 / 200 - 2x
a. What is the cost to remove 75% of the pollutant?
b. What is the cost to remove 90 % of the pollutant?
c. What is the cost to remove 99% of the pollutant?
d. For what value is this equation undefined?
e. Do the answers to sections a–d match your expectations? Why or why not?
(Source: Sea World https://www.seaworld.org/animal-info/info-books/flamingo/physical-characteristics.htm )
Q2. Biologists want to set up a station to test alligators in the lake for West Nile Virus. Suppose that the costs for such a station are $2,500 for setup costs and $3.00 to administer each test.
a. Write an expression that gives the total cost to test x animals.
b. You can find the average cost per animal by dividing total costs by number of animals. Write the expression that gives the average cost per animal.
c. Find the average cost per animal for 10 animals. 100 animals. 1,000 animals.
d. As the number of animals tested increases, what happens to the average cost to test the animals? Would the average cost ever fall below $3.00? If so, identify a value that supports your answer. If not, explain how you know.
e. How many animals should be tested for the average cost to be $5.00 per animal?
Q3. To estimate animal populations, biologists count the total number of animals in a small section of a habitat. The total population of animals is directly proportional to the size of the habitat (in acres) polled.
a. Write an equation using only one variable that could be used to solve for the constant of variation k.
b. A biologist counted the number of white tail deer in a 100 acre parcel of land in a nature preserve and found 12 deer. Find the constant of variation k.
c. If the entire nature preserve is 2,500 acres, then what is the total white tail deer population in the preserve? Describe how you arrived at your answer.
Part IV: Application Practice
Answer the following questions.
Hint for this problem: Pay attention to the units of measure. You may have to convert from feet to miles several times in this problem. You can use 1 mile = 5,280 feet for your conversions.
Q1. Many people know that the weight of an object varies on different planets, but did you know that the weight of an object on earth also varies according to the elevation of the object? In particular, the weight of an object follows this equation: w = Cr-2 , where C is a constant, and r is the distance that the object is from the center of the earth.
a. Solve the equation w = Cr-2 for r.
b. Suppose that an object is 100 pounds when it is at sea level. Find the value of C that makes the equation true. (Sea level is 3,963 miles from the center of the earth.)
c. Use the value of C you found in the previous question to determine how much the object would weigh in
i. Death Valley (282 feet below sea level)
ii. The top of Mt McKinley (20,430 feet above sea level)
Q2. The equation D = 1.2√h gives the distance, D, in miles that a person can see to the horizon from a height, h, in feet.
a. Solve this equation for h.
b. Long’s Peak in the Rocky Mountain National Park, is 14,255 feet in elevation. How far can you see to the horizon from the top of Long’s Peak? Can you see Cheyenne, Wyoming (about 89 miles away)? Explain your answer.
Part V: Application Practice
Answer the following questions.
Q1. Suppose you are an event coordinator for a large performance theater. One of the hottest new Broadway musicals has started to tour, and your city is the first stop on the tour. You need to supply information about projected ticket sales to the box office manager. The box office manager uses this information to anticipate staffing needs until the tickets sell out. You provide the manager with a quadratic equation that models the expected number of ticket sales for each day x. (x = 1 is the day tickets go on sale).
Tickets = -0.2x2 + 12x + 11
a. Does the graph of this equation open up or down? How did you determine this?
b. Describe what happens to the tickets sales as time passes?
c. Use the quadratic equation to determine the last day that tickets will be sold. (Note: Write your answer in terms of the number of days after ticket sales begin.)
d. Will tickets peak or be at a low during the middle of the sale? How do you know?
e. After how many days will the peak or low occur?
f. How many tickets will be sold on the day when the peak or low occurs?
g. What is the point of the vertex? How does this number relate to your answers in parts e and f?
h. How many solutions are there to the equation -0.2x2 + 12x + 11 = 0 ? How do you know?
i. What do the solutions represent? Is there a solution that does not make sense? If so, in what ways does the solution not make sense?
Provide complete and step by step solution for the question and show calculations and use formulas.