Problem 1. Deriving equations
a. Line A passes through the two points (6, 4) and (4, 6).
Find the equation of Line A.
What are the x - intercept and y - intercept of Line A?
b. The reciprocal of the slope of Line B is 0.25 and passes through the point (2, 3). Find its equation and write this equation in slope - intercept form.
c. What is the equation of Line A (from problem 1a) when its y - intercept is reduced by 4 units? Assume the new line is parallel to the initial line. What is the equation of Line B (from problem 1b) when its x - intercept is redu ced by 4 units? Assume the n ew line is parallel to the initial line.
Problem 2. Playing with two given equations.
Consider the following equations of two straight lines
i. y = x/5 + 4 and 0.2y = 4 - x
ii. y = 7x + 1 and y = 7x + 2
Answer the following questions for each of the above 2 sets of equations . Start with the two equations given in (i) and answer the next three questions; then, repeat for the two equations given in (ii).
a. What are the slopes, x - intercept and y - intercept of both lines?
b. Graph the two lines in a single graph measuring y on the vertical axis and x on the horizontal axis
c. At which co - ordinate point (x, y) do the two straight lines intersect?
[Hint: Be careful on this step when you are working with the equations given in (ii.)]
Problem 3. Adding equations
Consider the following two equations 2y = 6 - x and 3y = 18 – 2x
a. What are the intercepts on the X-axis and the Y-axis for these two equations?
b. Draw the graph of the two straight lines, and show graphically the graph of what you get when you add these two straight lines horizontally. Use three graphs: in the first graph draw the first line, in the second graph draw the second line, and in the third graph draw the graph that results when you add the two lines together horizontally. In your three graphs consider only the values found in the first quadrant of your coordinate graph (that is, only consider the positive values of x and y when graphing). c. What is the equation for the line(s) you drew in the third graph? (Hint: If you have more than one line you will need to provide a range of values for each equation.)
Part II: Opportunity Costs, Absolute Advantage, Comparative Advantage, Production Possibility Frontier (PPF)
Problem 4. Schmidt and Alex are employed as Librarians in College Library. At the end of each day, they have to deal with a number of returning books, B , and laptops, L . Their work consists of scanning the code bar stuck to either book or laptop, so that each item is discharged.
How quickly they can scan each item is given as below:
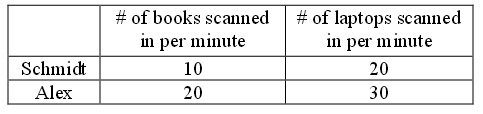
According to the information above, answer the following questions (a) - (e):
a. For Schmidt, what is the opportunity cost of scanning 1 book (remember that opportunity cost is measured in terms of the good that is given up)? What is opportunity cost of scanning 1 laptop for him? For both answers provide the units of measurement. Now, answer the same two questions for Alex.
b. Who has the comparative advantage in scanning books? Who has the comparative advantage in scanning laptops? In your answer provide a verbal explanation
c. Suppose Schmidt and Alex decide to specialize in the production of these two goods and then trade with one another to get the work done. If they do this what is the acceptable range of trading prices that they will both accept for a scanned book measured in terms of scanned laptops?
Suppose today Schmidt and Alex go to College Library very late so that they both have only 30 minutes to do their scanning work. Assume this constraint is true for questions (d) through (e).
d. In two separate graphs draw the PPFs of Schmidt and Alex measuring scanned books (B) on the vertical axis and scanned laptops (L) on the horizontal axis. Write an equation for Schmidt’s PPF and one for Alex’ s PPF in slope - intercept form and where you have assumed that each of these individuals have a total of 30 minutes time to scan either books or laptops. Label your graphs carefully and completely!
e. Draw a graph of the joint PPF between Schmidt and Alex and provide the coordinate values (L, B) for the kink point. Measure scanned books (B) on the vertical axis and scanned laptops (L) on the horizontal axis.
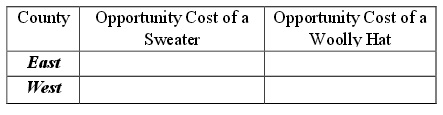
Problem 5. Suppose there are two counties in a southern state, East and West . Both counties could produce sweaters ( S ) and woolly hats ( H ) by weavers. Each county employs 10 weavers per year, and each weaver works for 2000 hours per year. Both East and West have linear production possibility frontiers in the production of sweaters and hats. By using up all the labour hours in a whole year, East could reach an infinite number of possible production bundles including these two: (3000 woolly hats, 1000 sweaters), or (5000 woolly hats, 0 sweaters); and West could reach an infinite number of possible production bundles including these twos: (4000 woolly hats, 500 sweaters), or (5000 woolly hats, 250 sweaters). Initially, county East and West are blocked by a giant mountain so that no trade takes place between them. According to the given information, answer the following questions (a) - (e):
a. What is the opportunity cost of each product for each county? Remember that each county faces a linear tradeoff (i.e. that the tradeoff is constant – the opportunity cost of producing the first sweater is the same as the opportunity cost of producing the second sweater and so forth). Fill out the table below.
b. Which county has the comparative advantage in producing woolly hats? Which county has the comparative advantage in producing sweaters?
c. Let S and H be the number of piece of sweater and woolly hat produced, respectively. Give the equations for the PPF of each county. (Measure S on the vertical axis and H on the horizontal axis)
d. From (c), draw on two separate graphs the PPF of each county with S measured on the vertical axis and H measured on the horizontal axis. Make sure your graphs are completely and carefully labelled. Which county has the absolute advantage in producing woolly hats? Which county has the absolute advantage in producing sweaters?
e. In each county, how many labor hours are needed to produce a woolly hat? And how many labor hours are needed to produce a sweater? Fill out the table below.

f. Suppose now that a tunnel has been successfully constructed through the mountain, thereby making it possible for East and West to trade and transport goods by train. Regardless of transportation cost, what is the acceptable range of trading prices for one sweater? Please explain your answer.
g. If the two counties cooperate in the production of woolly hats and sweaters, then which County should specialize in producing each good? Draw the (joint) PPF with S and H on the vertical and horizontal axes, respectively. Clearly mark the kink point and the two end points on the PPF.