Problem 1. Consider a perfectly competitive market with a market demand curve that is given by the equation P = 2000 - Q. A representative firm in this market has a total cost curve given by the equation TC = 121 + 64q + q2 and a marginal cost curve given by MC = 64 + 2q. Q is the market quantity and q is the firm quantity.
Let's start in the short-run with this market. Suppose the short-run price in this market is $100.
a. What is the market quantity in this market given this short-run price?
b. What is the representative firm's level of production given this short-run price?
c. What is the representative firm's level of profits in the short-run given this market price?
d. Can this short-run equilibrium also represent a long-run equilibrium for this firm? Explain your answer. What do you anticipate will happen as this market adjusts to the long-run?
e. Rounding to the nearest whole number, how many firms are operating in the short-run in this market given a market price of 100 firms?
Now, let's go to the long-run in this market. Let's assume that nothing happens to the market demand curve, but that the market has adjusted and is now at a long-run equilibrium.
f. Intuitively thinking, what do you expect to happen to the following in the long-run? Your answers should be "increase", "decrease", or "remain unaffected".
i. Market quantity
ii. Market price
iii. Firm quantity
iv. Firm price
v. Number of firms in the industry
vi. Level of profits for the firm
g. What is the break-even price in the long-run for a representative firm in this industry?
h. Assuming no change in the market demand for this product, what will be the long-run market quantity in this market?
i. How many firms will be in this industry in the long-run?
j. What happen to the number of firms in the industry in the long-run compared to the number of firms in the industry in the short-run?
k. What is the level of profit in the long-run for the representative firm?
l. Calculate the value of consumer surplus (CS), producer surplus (PS) and deadweight loss (DWL) in the long run. Hint: you will need to find the market supply curve for this one! And, that means you will need to do the horizontal summation of the individual supply curves in order to find the equation for the market supply curve.
m. Fill in the following table based upon this market being in long-run equilibrium.
Price in the market:
Total Quantity (Q) produced in the long-run:
Profit maximizing quantity (q) produced by the firm in the long-run:
Profit for the firm in the long-run:
CS in the market in the long-run:
PS in the market in the long-run:
DWL in the market in the long-run:
Problem 2. Consider a monopolist where the market demand for the good is given by the equation P = 1000 – Q and the total cost function for the monopolist is given by TC = 1000 + 100Q + (1/2)Q2 and the monopolist’s MC curve is given by the equation MC = 100 + Q.
a. What is the fixed cost of production for this monopolist?
Suppose this firm acts as a single price monopolist where it produces the profit-maximizing level of output based upon its being able to charge a single price for its product.
b. Given that the firm is a single-price monopolist, find the firm’s equilibrium output, equilibrium price, and level of profits.
c. Given that the firm is a single-price monopolist, find the value of consumer surplus (CS), producer surplus (PS), and deadweight loss (DWL) for the monopolist. Hint: to find the area of PS you will need to think about this as the sum of two areas: the sum of the area of a triangle plus the area of a rectangle-you find it helpful to draw a sketch of the monopolist’s demand curve, MR curve, and MC curve!
Now, let’s consider the same monopolist who decides to engage in second degree price discrimination. Suppose this monopolist will continue to produce the profit maximizing quantity and charge the profit maximizing price that they selected as a single price monopolist, but will, in addition, produce an additional 100 units of the good and sell these 100 units for a price of $600 per unit.
d. Find the firm’s level of profits, SC, PS, and DWL if they practice second degree price discrimination as described in the above information.
Now, suppose this monopolist is able to practice first degree price discrimination so that the monopolist charges each consumer the maximum price that consumer is willing to pay.
e. If this monopolist practices first degree price discrimination (that is, perfect price discrimination) its demand curve is also the firm’s MR curve. Explain why this is true.
f. Given this firm practices first degree price discrimination, calculate the value of the firm’s profit, CS, PS and DWL.
g. Fill in the table below with your findings from this problem (this will make it easier to compare the costs and benefits of price discrimination).
Single Price Second Degree Price First Degree Price
Monopolist Discrimination Discrimination or
Perfect Price
Discrimination
Profit
CS
PS
DWL
h. From a profit maximizing perspective, which of the three options in this question is best for the monopolist? Explain your answer.
i. From a consumer’s perspective is there anything beneficial about perfect price discrimination? Explain your answer.
Problem 3. Suppose the following graph represents a natural monopoly.
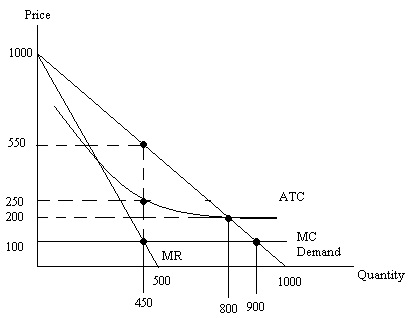
a. Suppose this natural monopoly is allowed to act as a single price monopolist without regulation. What will be the monopolist’s price for the good, its total output, and its profit?
b. Suppose this natural monopoly is regulated so that it breaks even. What will be the monopolist’s price for the good, its total output, and its profit if it is regulated in this manner?
c. Suppose this natural monopoly is regulated so that it produces the socially optimal amount of output, or in other words, so that it produces the allocatively efficient amount of output. What will be the monopolist’s price for the good, its total output, and its profit if it is regulated in this manner? Will the monopolist be willing to produce under this regulatory program?
Problem 4. Suppose there are two classes of buyers in a market served by a monopolist. At this point the two classes are lumped together and the monopolist is currently producing the profit maximizing quantity based upon being a single price monopolist. Suppose that the monopolist perceives that its relevant market demand curve is given by the equation P = (40/3) – (2/3)Q and its MC = ATC = 4.
a. Suppose this monopolist acts as a single price monopolist. Calculate the monopolist’s price, quantity, and profit given the above information.
Now, suppose that the monopolist realizes that the two classes of buyers have different demand curves and that the first class of buyers demand curve is given by the equation P = 10 – Q while the second class of buyers demand curve is given by the equation P = 20 – 2Q. Assume for the rest of this problem that this monopolist will practice third degree price discrimination and will charge different prices for consumers in the two different classes of buyer.
b. In the first class of buyer what quantity of the good will be provided, what price will consumers pay, and what will be the level of profits for this class of buyer?
c. In the second class of buyer what quantity of the good will be provided, what price will consumers pay, and what will be the level of profits for this class of buyer?
d. What is the total amount of profit that the monopolist receives when the monopolist practices third degree price discrimination? How does this level of profit compare to the level of profit the monopolist receives when it sells its output at a single price?
e. For practice, find the monopolist’s market demand curve based upon the two classes of buyers. You will have multiple linear segments for this market demand curve and you will need to specify the relevant range for each demand curve segment.