Problem 1. In this question the goal is to compare a perfectly competitive industry to a monopoly. For the comparison we will assume that both the perfectly competitive industry and the monopoly have the same market demand curve and market supply curve. For our example the market demand and market supply curves are given as
Market Demand: P = 1000 – Q
Market Supply: P = Q
a. Assume that the industry is perfectly competitive. What is the long-run equilibrium price and quantity in this industry?
b. Assume that the industry is perfectly competitive. What is the value of consumer surplus when the industry is in long-run equilibrium? What is the value of producer surplus when the industry is in long-run equilibrium?
c. Assume that the industry is now a monopoly. What is the long-run equilibrium price and quantity in this market?
d. Compare the equilibrium price and quantity found in part (a) with the equilibrium price and quantity found in part (c).
e. Assume that the industry is now a monopoly. What is the value of consumer surplus when the monopoly is in long-run equilibrium? What is the value of producer surplus when the monopoly is in long-run equilibrium? Round your answers to the nearest whole number.
f. Assume that the industry is now a monopoly. What is the deadweight loss that occurs due to this industry being a monopoly? How is this deadweight loss related to the consumer surplus and producer surplus you calculated in part (d)? Round your answer to the nearest whole number.
g. Verify that the sum of consumer surplus, producer surplus and deadweight loss for the monopolist is approximately equal to total surplus for the perfectly competitive industry.
Problem 2. Suppose there is a market that provides electricity to a large metropolis. The graph below represents the market’s demand curve, the average total cost of providing electricity to the metropolis for a representative firm, and the marginal cost cure for the market.
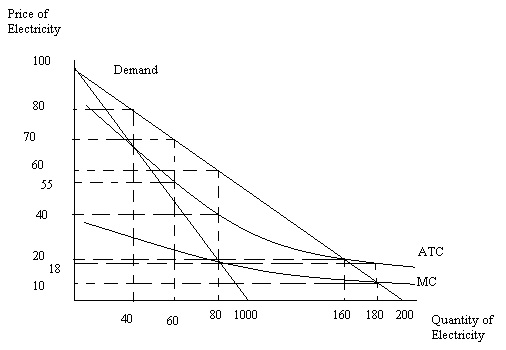
a. Suppose that we want this market to produce the socially optimal amount of the good. Furthermore, suppose we identify the socially optimal amount of the good as being that amount of the good where the price the consumer pays for the last unit of the good is exactly equal to the marginal cost of producing that last unit of the good. What is the socially optimal amount of the good?
b. Suppose that the socially optimal amount of the good identified in part (a) is produced. What is the cost of producing the good if the total amount is produced by a single firm?
c. Suppose that the socially optimal amount of the good identified in part (a) is produced. What is the total cost of producing this level of output if there are three equal size firms that divide up the market evenly and each produce 1/3 of the total amount provided.
d. Compare your answers in parts (b) and (c). Generalize your finding and why it is relevant.
Problem 3. Use the same graph that you used in problem 2 to answer this set of questions.
a. If this industry acts like a monopoly, what will be the equilibrium price and quantity in the market? What will be the level of profits?
b. Suppose this industry is regulated as a natural monopoly and the regulators set price so that the natural monopolist produces the socially optimal amount of output. What will be the price, quantity, and level of profits for the natural monopoly given this type of regulation? What must the natural monopoly receive from the government in order to be willing to produce the socially optimal amount of the good?
c. Suppose this industry is regulated as a natural monopoly and the regulators set price so that the natural monopolist breaks even. What will be the price, quantity, and level of profits for the natural monopolist given this type of regulation?
Problem 4. Suppose there is a market that has two firms operating in it and both Firm A and Firm B are aware of each other. The two firms have decided to collude and divide up the market evenly. Suppose that the market demand curve is given by the equation P = 30 – Q and the marginal cost curve for producing the good is given as MC = $2/ unit of the good. Furthermore, there are no fixed costs of production.
Initially the two firms decide to produce the profit maximizing quantity for the market and then divide this production evenly between the two firms.
a. What quantity will each firm produce given this arrangement?
b. What price will be charged for the good?
c. What will the level of profit for each firm?
d. What is the total amount of profit from producing this good?
Now, suppose that firm A has decided to undercut the agreement and sell the good for $14 a unit. Firm B is going to maintain its price at the level that was established when both firms agreed to evenly divide the market.
e. What quantity will be produced by Firm A now that Firm A is willing to sell the good for $14?
f. What quantity will be produced by Firm B now that Firm A is willing to sell the good for $14?
g. What is firm A’s profit?
h. What is firm B’s profit?
Now, suppose that both Firm A and Firm B drop the price of the good to $14 per unit.
i. What is firm A’s profit if both Firm A and Firm B drop the price of the good to $14 per unit?
j. What is firm B’s profit if both Firm A and Firm B drop the price of the good to $14 per unit?
k. Fill in the matrix below using the information you calculated in this problem. Enter firm A’s profit as the first entry and firm B’s profit as the second entry.

l. Given your matrix in part (k), what do you predict will be the outcome in this market?
Problem 5. Suppose there is a market characterized by the following demand and supply curves:
Demand: P = 10 – Q
Supply: P = Q
a. What is the equilibrium price and quantity in this market?
b. What is the value of Consumer Surplus (CS), Producer Surplus (PS), and Total Surplus (TS) in this market?
Now, suppose that there is a negative externality of $2 per unit in this market that is not corrected for by the market.
c. What is the total externality cost to this society given the level of production you found in part (a)?
d. What is the value of the TS once you subtract out this externality cost? That is, what is the net TS?
Now, suppose that an excise tax of $2 per unit is levied on this good (producer’s are legally responsible for the tax) in order to correct for the negative externality.
e. What will be the new price and quantity in this market once this tax is imposed?
f. What is the value of tax revenue? What is the value of CS and PS now that the excise tax has been imposed? What is the sum of CS, PS and tax revenue (this is the new TS with the tax-just remember that the government has captured some of the consumer and producer surplus)?
g. What is the total externality cost to this society given the level of production you found in part (e)?
h. What is the value of the TS once you subtract out this externality cost?
i. If the excise tax is not imposed, what is the deadweight loss to society from the externality?
Problem 6. Suppose there are two people, Sarah and Jim, who live in a community. This community is trying to decide the optimal amount of lighthouses to build. Both Sarah and Jim often boat and know that getting back to harbor is hard in their community since the shoreline is rocky and there are many treacherous currents. Assume for the sake of this problem that there are no other people who need to navigate the waters of this community.
a. Are lighthouses a private or a public good? Explain your answer making sure you comment on the properties of non-rivalness and non-excludability.
Suppose that Sarah’s demand for lighthouses is given by the equation
Ps = 10 – Qs
while Jim’s demand for lighthouses is given by the equation
Pj = 30 – 3Qj
b. What is the market demand curve for this good?
We will assume that this market demand curve is the same as the marginal social benefit curve (MSB curve) for lighthouses. That is, there are no consumption side externalities associated with these lighthouses.
Furthermore, you also know that the marginal social cost curve (MSC curve) for lighthouses is given by the equation
MSC = Q
c. Given this information, what is the socially optimal amount of lighthouses to produce in this community? What will be the total price per lighthouse if the community produces the socially optimal amount of lighthouses?
d. What price per lighthouse will Sarah pay if the socially optimal amount of lighthouses is produced?
e. What price per lighthouse will Jim pay if the socially optimal amount of lighthouses is produced?