Question1) a) Let M and T be a metro city and a nearby district town, respectively. Our government is trying to develop infrastructure in T so that people shift to T. Each year 10% of T’s population moves to M and 1% of M’s population moves to T. What is the long term effect of this on the populations of M and T? Are they likely to stabilise?
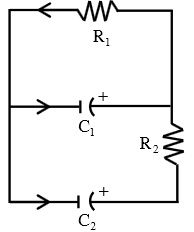
b) The circuit in Figure 1 is given by the matrix equation
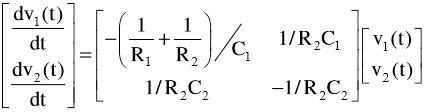
where v1(t) and v2 (t) are the voltages across the capacitors C1 and C2 at time t. Suppose the resistor R1 is 1 ohm, R2 is 2 ohms, C1 is 1 farad, C2 is 0.5 farad, there is an initial charge of 5 volts on C1 and 4 volts on C2 . Then solve the equation.
c) Give an example each to show that the following statements are false.
i) If A1 and A2 are n × n matrices which are similar to B1 and B2 , respectively, then A1 A2 is similar to B1 B2 .
ii) Two n n ×matrices with the same characteristic polynomial mu st be similar.
Question2) Find a unitary matrix U such that * U AU is upper triangular, where A=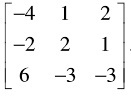
Hence obtain an orthonormal basis for the linear operator T on R3 with respect to which the matrix of T is upper triangular. Here T is defined by A w.r.t. the standard orthonormal basis on R3.
Question3) Find the least squares solution to Ax = b, where A=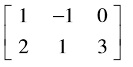
, b=[-4 3]t by
i) using the SVD of A.
ii) solving the system At Ax = Atb