Discuss the below in detail:
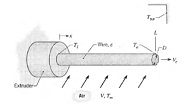
Q: In an extrusion process, copper wire emerges from the extruder at a velocity V e and is cooled by convection heat transfer to air in cross flow over the wire, as well as by radiation to the surroundings.
(a) By applying conservation of energy to a differential control surface of length dx, which either moves with the wire or is stationary and through which the wire passes, derive a differential equation that governs the temperature distribution. T(x), along the wire In your derivation, the effect of axial conduction along the wire may be neglected. Express your result in terms of the velocity, diameter, and properties of the wire (Ve, D, p, cp, e), the convection coefficient associated with the cross flow (h), and the environmental temperatures (T8, Tsur)
(b) Neglecting radiation, obtain a closed form solution to the foregoing equation. For V e = 0.2 m/s, D = 5 mm, V = 5 m/s, T8 = 25°C, and an initial wire temperature of Ti = 600°C, compute the temperature To of the wire at x = L = 5 m. The density and specific heat of the copper are p = 8900 kg/m3 and c p = 400 J/kg · K, while properties of the air ma) be taken to be k = 0.037 W/m · K, v = 3 x 10-5 m2 /s, and Pr = 0.69.
(c) Accounting for the effects of radiation, with e = 0.55 and Tsur = 25°C, numerically integrate the differential equation derived in part (a) to determine the temperature of the wire at L = 5 m. Explore the effects of V e and ?L on the temperature distribution along the wire.