Untied and Air ’R’ Us are the only two airlines operating flights between Collegeville and Bigtown. That is, they operate in a duopoly. Each airline can charge either a high price or a low price for a ticket. The accompanying matrix shows their payoffs, in profits per seat (in dollars), for any choice that the two airlines can make.
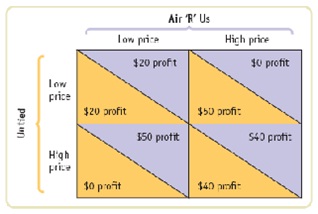
a. Suppose the two airlines play a one-shot game—that is, they interact only once and never again. What will be the Nash (noncooperative) equilibrium in this one-shot game?
b. Now suppose the two airlines play this game twice – therefore two payoffs to add up each time. And suppose each airline can play one of two strategies: it can play either “always charge the low price” or “tit for tat”— that is, it starts off charging the high price in the first period, and then in the second period it does whatever the other airline did in the previous period. Write down the payoffs to Untied from the following four possibilities:
i. Untied plays “always charge the low price” when Air ’R’ Us also plays “always charge the low price.”
ii. Untied plays “always charge the low price” when Air ’R’ Us plays “tit for tat.”
iii. Untied plays “tit for tat” when Air ’R’ Us plays “always charge the low price.”
iv. Untied plays “tit for tat” when Air ’R’ Us also plays “tit for tat.”