Problem 1: As part of a fractious breakup, Dana and Blair have recently sold their joint possession, an electric keyboard, for $200. They now are arguing about how to split the proceeds of the sale. In order to reach a conclusion, they have enlisted the services of Mordecai the Mediator. Mordecai proposed the following solution: "I want eash of you, seperately and independently, to write on a slip of paper the number of dollars that you would like to keep for yourself (XD and XB). If XD + XB is less than or equal to $200, then you can each keep the figure you name and I'll take the rest [ie. $200 - XD + XB] as my mediation fee. If XD + XB > $200, then I will keep the entire $200."
a) Identify the Nash equilibrium (or equilibria) for this one-shot simultaneous-move game. Explain your reasoning.
b) What do you think would be the most likely outcome of this game? Briefly explain.
Problem 2: Firms I and II are duopoly producers of differentiated products. In each period, the profits for each firm depend on the pricing decisions of both, as given in the following table.
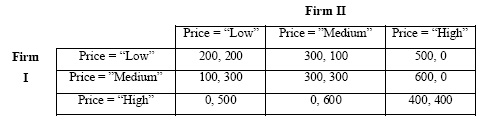
a) Identify the one-shot, simultaneous-move pure-strategy Nash equilibrium or equilibria for this game.
b) Assume that each firm [i=I,II] maximizes the geometrically-discounted present value of the infinite sum of its expected current and future payoffs. Assume also that both firms follow strategies incorporating a "tough trigger" enforcement mechanism, defined by "Charge the 'High' price as long as both firms charged a 'High' price in the previous period; otherwise charge the 'Low' price forever after." For what values will these strategies specify a repeated-game Nash equilibrium?
c) Repeat your results from part c) if the firms instead adopt strategies incorporating a "mild trigger" enforcement mechanis, defined by "Charge the 'High' price as long as both firms charged a 'High' price in the previous period; otherwise charge a 'Medium' price forever after." Is it more likely that Firm I and Firm II will be able to sustain cooperation with this more lenient enforcement strategy? Briefly explain.