Model of a population with diffusion

Question

Q1. Solve the following 1D heat conduction equation by pen and paper.

∂u/∂t = 4 ∂²u/∂x², u(0,t) = 10, ∂u/∂x|(1,t) = 0, u(x,0) = 2

Q2. Find the solution of the following 1D wave equation by pen and paper.

∂²u/∂t² = 9 ∂²u/∂x², u(0,t) = 0, y(1,t) = 0, u(x,0) = f(x), ∂u/∂t|(x,0) = g(x)

Q3. Population model: A growth model of a population with diffusion is given by the following:

∂N/∂t = αN(1 - N/k) + D ∂²u/∂x²

Where, N > 0 is the population and α, k, D > 0 are parameters.

i) Find the homogeneous steady state(s) (including zero)

ii) Perform linear stability analysis about the equilibrium point (s) for the non-diffusive system and obtain the condition for stability.

iii) Perform the linear stability analysis for diffusive system and conclude about the effect of diffusion on the system.

Q4. Reaction diffusion model: A reaction diffusion model is given as follows:

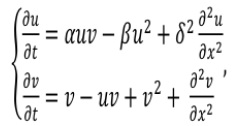
where, u, v > 0 are concentrations and α, β > 0 are parameters.

i) Find the non-zero equilibrium point(s).

ii) Obtain the condition for diffusive instability and evaluate the values of δ for which diffusive instability can take place.