Minimum critical euler axial compression

Question

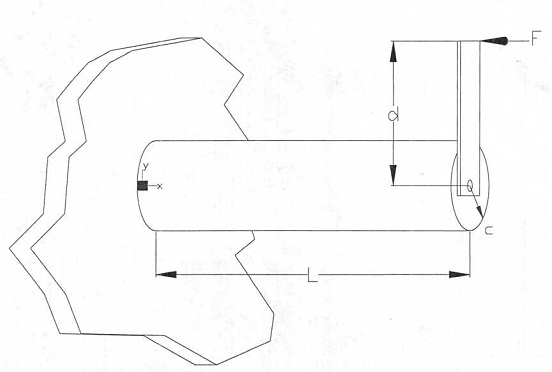
Problem 1: Calculate the bending  (σ_x) and shear stress (τT_xy) at the surface element shown on the solid circular shaft below. Use Mohr's circle to calculate the principle stresses, σ₁, σ₂ the maximum shear stress on the element, τ_max and the angle, θ, between the plane shown and the plane of principle stresses. Use the following data:

F = 20 kips
d = 16 in
L = 6 ft
c = 3 in
E = 29000 ksi
G = 11200 ksi

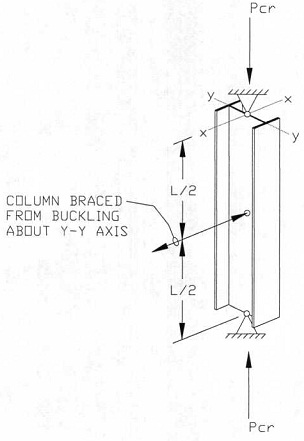
Problem 2: Calculate the minimum critical Euler axial compression force, σ_cr and the minimum critical Euler axial compression stress, σ_cr, for the column below which is pinned at the top and bottom ends and braced as shown. Use the following properties....

A = 12 in²  
l xx   = 300 in⁴  
I ri   = 50 in⁴  
L = 20 ft
E = 29,000 ksi

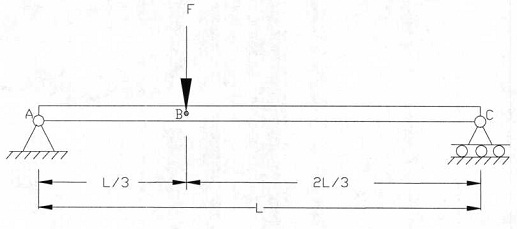
Problem 3: Derive the equations of the elastic curve and use them to calculate the deflection and rotation at point B in terms of E, I, F and L.

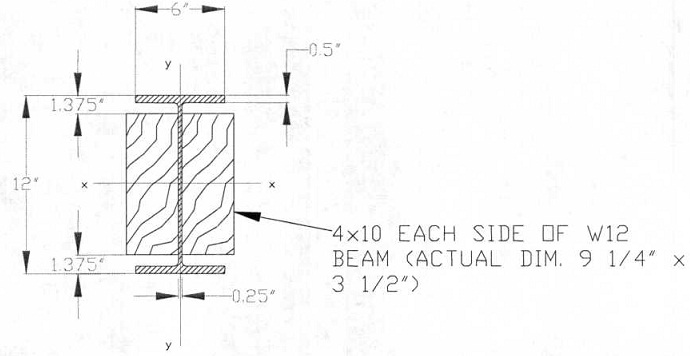
Problem 4: Calculate the maximum bending stress in the  wood AND steel of the composite section shown below, knowing:

E_w = 1875 ksi
E_s = 29000 ksi
M = 400 in-kip

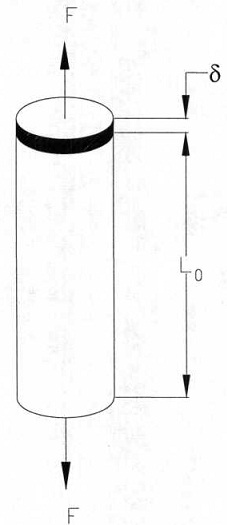
Problem 5: The round tensile specimen shown below has a diameter of 0.5 in. A load, F, is applied and the deflection, δ, is measured. Given the following:

d = 0.5 in
L_o = 10 in
F = 5 kip
g = 0.022 in

Calculate E (elastic modulus) for the material of the specimen. Also, calculate the axial tension, σ_u, in the specimen and the engineering axial strain, ε. Assume that stresses and strains are in the elastic range of the stress-strain diagram.