Matrix multiplication and skew-symmetric matrices

Question

Problems:

Matrix Symmetry, Matrix Multiplication and Skew-Symmetric Matrices

1.  Compute the product by inspection.

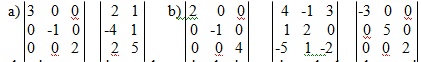
2.  Use the given equation to determine by inspection whether the matrices on the left commute.

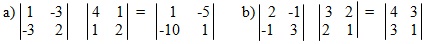
3.  Let A be an n x n symmetric matrix.

a) Show that A^k is symmetric is k is any nonnegative integer.  Do in a proof.

b) If p(x) is a polynomial, is p(A) necessarily symmetric?  Explain.  Do in a proof.

4.  A square matrix A is called skew-symmetric if A^T = -A.  Prove:

a) If A is an invertible skew-symmetric, then A^-1 is skew-symmetric.

b) If A and B are skew-symmetric, then so are A^T, A + B, A - B, and kA for any scalar k.

c) Every square matrix A can be expressed as the sum of a symmetric matrix and a skew-symmetric matrix. 

Hint:  Note the identity A = ½ (A + A^T) + ½ (A - A^T).

5.  Indicate whether the statement is always true or sometimes false.  Justify each answer in proof.

a) If AA^T is singular, then so is A.

b) If A + B is symmetric, then so are A and B.

c) If A is an n x n matrix and Ax = 0 has only the trivial solution, then so does A^Tx = 0.

d) If A² is symmetric, then so is A.