Questions:
Question (1)
Given, f(x) = ( x + 2 )(2x – 3) , f (– 2 ) = ?
(a) 0
(b) 4
(c) -6
(d) -14
Question (2)
The equation of the line through (8 , 6 ) and (2 , - 4) is
a. 5x - 3y = 22
b. y = 3/5x + 8/5
c. 3x + 4y = 48
d. -4x + 2y = -16
Question (3)
A Revenue function is R(x) = 22x and a cost function is C(x) = – 9x + 341.
The break-even point is
(a) (17 , 374)
(b) (242 , 9)
(c) (11 , 242 )
(d) (31.5 , 661.5)
Question (4)
An item costs $1300 , has a scrap value of $100, and a useful life of six years.
The linear equation relating book value and number of years is
(a) BV = -100 x + 1300
(b) BV = -100 x + 1200
(c) BV = -200 x + 1200
(d) BV = -200 x +1300
Question (5)
The solution to the system of equations
x + 3y = 12 , 4x – y = – 17 is
(a) (3 , 3)
(b) (12 , -17)
(c) (- 3, 5)
(d) (5 , 3)
Question (6)
The augmented matrix 1 3 2 | 4 represents the system of equations.
2 -1 5 |-2
-3 1 6 | 1
(a) x1 + 3x2 + 2x3 + 4x4 = 0 (b) x1 + 3x2 + 2x3 = 4
2x1 – x2 + 5x3 – 2x4 = 0 2x1 – x2 + 5x3 = -2
-3x1 + x2 + 6x3 + x4 = 0 – 3x1 + x2 +6x3 = 1
(c) x1 + 2x2 – 3x3 = 4 (d) x1 + 3x2 + 2x3 = 0
3x1 – x2 + x3 = -2 2x1 – x2 + 5x3 = 0
2x1 + 5x2 + 6x3 = 1 -3x1 + x2 + 6x3 = 0
Question (7)
The following matrix is obtained from the augmented matrix of a system of equations.
1 0 3 |20 . The solution to the system is
0 1 2 |-2
0 0 1 | 4
(a) No solution
(b) (20 , -2 , 4 )
(c) ( 3 , 2 , 1 )
(d) ( 8 , -10 , 4 )
Question (8)
A = [2 -1] , B = [4 -2] Find 3A-B.
[3 0] [5 1]
A. [2 -1]
[4 1]
B. [-6 3]
[-6 3]
C. [6 -3]
[9 0]
D. [10 -5]
[14 -1]
Question (9)
For the input-output matrix A, find the output required to meet the demand D.
A = [0.2 0.4] , D = [ 700]
[0.3 0.6] [ 400]
A.[ 200 ]
[ 150 ]
B.[ 2200 ]
[ 2650 ]
C.[ 300 ]
[ 450 ]
D.[ 1250 ]
[ 3750 ]
Question (10)
Select the point which is in the feasible region of the system of inequalities.
4x + y < 8
2x + 5y < 18 , x > 0 , y > 0
(a) (2 , 4)
(b) (- 1 , 2 )
(c) ( 1 , 3)
(d) (4 , 1 )
Question (11)
The maximum value of z = 20x + 8y subject to
3x + y < 24
6x + 4y < 66 , x > 0 , y >0 is
(a) 220
(b) 160
(c) 172
(d) 132
Question (12)
The minimum value of z = 5x + 15y , subject to the constraints
4x + 3y > 72 , 6x + 10y < 174 , x > 0 , y > 0 occurs at
(a) (0 , 17.4)
(b) (9 , 12)
(c) (18 , 0 )
(d) (29 , 0)
Question (13)
Find the maximum value of z = 6x + 10y in the feasible region shown
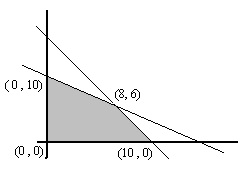
(a) 108 at (8 , 6)
(b) 130 at (8 , 6)
(c) 108 at (10, 0)
(d) 130 at (0 , 10)
Question (14)
Pivot on the appropriate entry to find the next tableau
|
2 1 2 1 0 0 0 330
|
|
1 2 2 0 1 0 0 330
|
|
-2 -2 1 0 0 1 0 132
|
|
-1 -2 -3 0 0 0 1 0
|
A.
|
1 1/2 1 1/2 0 0 0 165
|
|
-1 1 0 -1 1 0 0 0
|
|
-3 -5/2 0 -1/2 0 1 0 -33
|
|
2 -1/2 0 3/2 0 0 1 195
|
B.
|
1 -1 0 1 -1 0 0 0
|
|
1/2 1 1 0 1/2 0 0 165
|
|
-5/2 -3 0 0 -1/2 1 0 -33
|
|
1/2 1 0 0 3/2 0 1 495
|
C.
|
6 5 0 1 0 -2 0 66
|
|
5 6 0 0 1 -2 0 66
|
|
-2 -2 1 0 0 1 0 132
|
|
-7 -8 0 0 0 3 1 396
|
Question (15)
Minimize z = 8x1 + 4x2 + 9x3 , subject to x1 + 2x2 + 5x3 > 40
3x1 + 4x2 + x3 > 50
2x1 + 6x2 + 7x3> 60
x1 > 0 , x2 > 0 , x3 > 0
the initial tableau for the dual problem is
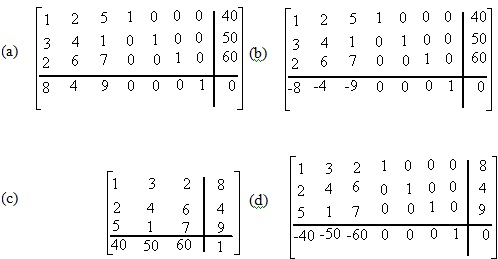
Question (16)
Set up the initial simplex tableau for the following problem.
Maximize z = 8x1 + 12x2
subject to 6x1 + 5x2 < 30
2x1 + 3x2 > 15
x1 + 2x2 = 6 , x1 > 0 , x2 > 2
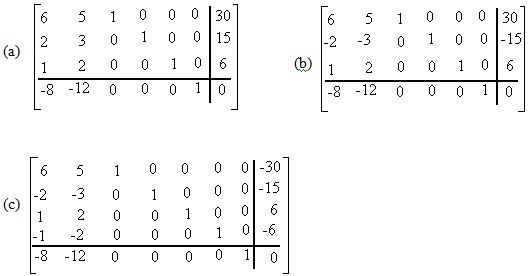
Question (17)
This is a tableau from a linear programming problem
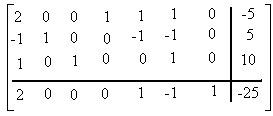
The information in the tableau indicates the linear programming problem has:
(a) a unique solution
(b) multiple solutions
( c) unbounded solutions
(d) no feasible solution
Question (18)
The feasible region of a maximization problem shown is determined by:
12x + 5y < 180,
5x + 4y < 98,
x > 0,
y > 0
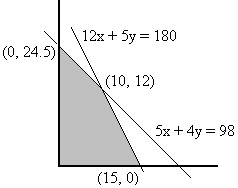
Which of the following objective functions has its maximum value at (0 , 24.5) ?
(a) z = 26x + 20y
(b) z = 32x + 16y
(c) z = 20x + 25y
(d) z = 24x + 8y
Question (19)
Find the length of a simple interest loan with P = $ 640 , r = 8.5% , and I = $ 95.20
(a) 18 months
(b) 2 years
(c) 11 months
(d) 1.75 years
Question (20)
How much should be invested t 8% compounded semiannually in order to have $ 5000 at the end of 8 years.
(a)$4215.27
(b) $9364.91
(c) $2669.54
(d) $3048.78
Question (21)
The future value of an annuity is A = $32,000. Periodic payments are made quarterly for four years and the annuity earns 8% compounded quarterly. Find the periodic payments.
(a) $ 422.40
(b) $ 1,716.80
(c) $2,000.00
(d) $2160.00
Question (22)
{x / x is a letter of the word SEEDED }∩{ x / x is a letter of the word DRESSED } =
(a) { S , E, D}
(b) {D, R, S}
(c) {D, R, E, S}
(d) { E }
Question (23)
If n(A) = 22, n(B) = 13, and n(A∩B) = , then n(AUB) = _____
(a) 35
(b) 28
(c) 29
(d) 27
Question (24)
A group of people consists of 14 men and some women. One man and one woman can be selected in 252 ways. There are ____ women in the gourp
(a) 238
(b) 18
(c) 16
(d) 152
Question (25)
A store selects four items from a selection of 6 items to arrange in a display. How may different arrangements are possible ?
(a) 15
(b) 24
(c) 360
(d) 6
Question (26)
How many ways can three prints be selected from a collection of 10 prints ?
(a) 120
(b) 720
(c) 30
(d) 72
Question (27)
The sample space of an experiment is {A, B, C, D} and P(A) = 0.1 , P(B) = 0.3 ,
P(C) = 0.4 , P({A , C}) =
(a) 0.4
(b) 0.5
(c) 0.6
(d) 0.8
Question (28)
If the probability that at least one person makes an A on the final exam is 0.15, then the probability that no one makes an A is
(a) 0.15
(b) 0.65
(c) 0.85
(d) 0
Question (29)
For two sets E and F , n(E) = 30, n(F) = 25, and n(E∩F) = 6. Then, P(E / F) = _____
(a) 25/30
(b) 6/25
(c) 6/30
(d) 6/55
Question (30)
A student applies for two different scholarships. The probability of receiving the first scholarship is 0.3 and the probability of receiving the second is 0.4. The dectisions are made independently. Find the probability the student receives exactly one scholarship
(a) 0.12
(b) 0.42
(c) 0.46
(d) 0.40
Question (31)
Estimate the population standard deviation of the grouped data
Score Frequency
1 - 3 1
4 - 6 6
7 - 9 3
A. √6.0
B. √5.6
C. √3.24
D. √4.24
Question (32)
For the following probability distribution µ = _________
Xi 250 300 400
Pi 0.30 0.50 0.20
a. 0.50
b. 300
c. 305
d. 317
Question (33)
For a sample size of n = 100, proportion p = 0.6 , and at a 95% confidence level, the upper bound of the proportion is
(a) 0.096
(b) 0.696
(c) 0.050
(d) 0.025