Assignment:
Matrix Algebra
Investment Allocation Problem
Donald Trump has some pocket change he wants to invest to make $3380. His stock broker suggested four (4) investment possibilities to accomplish this goal. The investments and their expected yields are listed in the table below.
|
Investment
|
Rate of Return
|
Risk Level
|
|
Magellan Stock Fund
|
12%
|
Medium
|
|
Fidelity Stock Fund
|
15%
|
High
|
|
NY City Bond Fund
|
7%
|
Low
|
|
Fidelity Fixed Income Fund
|
5%
|
Low
|
The total amount to be invested is $40000, and because "The Don" is concerned about risk, he only wishes to invest $13500 in stock funds, and the rest in lower risk funds. To keep risk even lower, his broker suggested investing half of the amount invested in Fidelity Stock into the Magellan Stock Fund. In other words, $0.50 in the Fidelity Stock Fund for every $1 invested in the Magellan Fund. How much should Mr. Trump invest on each fund to achieve his financial goal?
To solve this problem, we start by creating a linear system of four equations and four unknowns. Let x1, x2, x3, and x4 correspond to the investment amount on Magellan, Fidelity, NY City Fund, and the Fidelity Fixed Income Fund, respectively. Then, we write the equations with the information provided:
|
Investment Constraint
|
Equation
|
|
The sum of all investments must be $40,000:
|
x1+x2+x3+x4 = 40000
|
|
Return on investment must be $3380:
|
0.12x1+0.15x2+0.07x3+0.05x4=3380
|
|
Amount in low-risk funds must be $26500:
|
x3+x4=26500
|
|
$0.50 in Fidelity for every $1 in Magellan:
|
x1-2x2=0
|
This linear system of equations can be written in augmented matrix form:
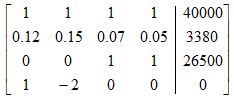
To complete the problem, use Gauss-Jordan elimination to find the solution vector X=
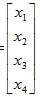
. In the process, you should show your work neatly. If you used the X=A-1B approach using a computer or a calculator, make sure to explain all steps leading to the answer.
Provide complete and step by step solution for the question and show calculations and use formulas.