Leasing Optimization
Web Mercantile sells many household products through online catalog. The company needs substantial warehouse space for storing its goods. Plans are now being made for leasing warehouse storage space over the next three months. Just how much space will be required in each of these months is known.
However, since these space requirements are quite different, it may be more economical to lease only the amount needed each month on a month-by-month basis. On the other hand, the additional cost for leasing space for additional months is much less than for the first month, so it may be less expensive to lease the maximum amount needed for the entire three months. Another option is the intermediate approach of changing the total amount of space leased (by adding a new lease and/or having an old lease expire) at least once but not every month. For instance, it may be more beneficial to lease some space for a leasing period of three months and some space for a leasing period of one month in month
1, lease some space for a leasing period of two months in month 2, and lease some space for a leasing period of one month in month 4.
The space requirement and the leasing costs for the various leasing periods are as follows:
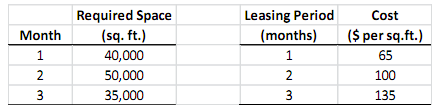
The objective is to minimize the total leasing cost for meeting the space requirements by determining how much space to lease for how many months for each possible leasing period in each month. For instance, in month 2, you have two possible leasing periods: 1 month or 2 months, because if you lease for 3 months in month 2, you will be leasing some space for the fourth month, which is not needed.
a) Mathematically formulate a linear programming model for the problem.
b) Formulate and solve a spreadsheet model for the problem.