Markov process and irreducible matrix

Question

Question 1:

a) Describe about Markov process, ergodic chain and irreducible matrix?

b) which of the given matrices are stochastic?

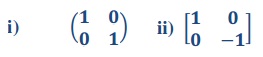
Question 2:

a) state and prove changing stakes result x₂

b) If p = 1/3, q = 1/2, z =1, a = 1000 prove that d_z = 999.

Question 3:

a) A fair coin is tossed repeatedly. If X_n denote the maximum number of numbers occurring in the first n tosses, find the transition probability matrx P of the Markov chain. Also find P² and P (X₂ = 6)

b) which of the given matrices are regular.

Question 4: Three boys A, B and C are throwing a ball to each other. A always throws the ball to B and B always throws to C; but C is just as likely to throw the ball to B as to A. Show that the process is Markovian. Find out the transition matrix and categorize the states.