Problem 1. Market Demand and Supply (Hint: this question is a review of material you should have seen and learned in Economics 101.) Suppose the market for snowshoes in Wiscons in is perfectly compe titive. The market supply of snowshoes in the market is given by the equation P = Q where P is the price per pair of snowshoes and Q is the quantity of pairs of snowshoes. The demand for snowshoes by consumers in Madison is given by the equation P = 12 – Q, and the demand by consumers in Milwaukee is given by the equation P = 4 – 1/2Q.
(a) If the only consumers for snowshoes in Wiscons in live in Madison or Milwaukee, what is the market demand for snowshoes in Wisconsin?
(b) What is the equilibrium price and quantity in the market for snowshoes?
Problem 2. Graphing lines from points and us ing models to evaluate a policy In the real world, firms and the government often do not know consumer demand. So, say a monopolist firm has experimented with different prices and recorded the quantities sold. Assume that all of these are points on the same demand curve. And that, after this experimentation, the monopolist learns the true demand curve, but the government does not know the true demand curve. You can assume in this problem that the government does have access to the information in the table below.
Price Quantity
24 1
21 2
The government would like to implement a unit or excise tax of T dollars per unit of output (possibly, a negative tax, or subsidy) so th at the firm produces 3 units of output.
(a) Based on this information, the government wants to guess a linear demand curve that goes through both of these points. What is the equation of the guessed demand curve written in y-intercept form (this form of the equation is the inverse demand curve): P = a + bQ (find: a and b )?
(b) Say, the monopolist has marginal cost: MC = Q (and the government knows this). Recall that for a linear demand curve in the form P=a+bQ , a monopolist's marginal revenue is MR=a+2bQ. A profit-maximizing firm produces where MR = MC + T . So, say the government believes the demand is given by th e line you found in part (a), and wants the firm to produce 3 units of output. What tax does th e government decide to charge given this information?
(c) When it implements this tax, to the government's surprise, the firm sells 2.3 units and charges a price of $19.45 (what the consumer pays). Is th is what the experimental linear demand predicted? Plot the three points you now have for the demand function and connect each point with a line segment (you do not have to be that precise with the graph). What is the rough shap e of the function you have drawn?
(d) Suppose the true demand curve in slope in tercept form is given by the equation: P = (5- Q)(5+Q) . Find the true tax T needed to ensure an output of 3 units.
Hint: the optimal output for the firm as a function of the tax T solves the following quadratic equation: (25-T) – Q – 3Q2 = 0. Also, since the demand equation is different, the MR equation will also be different: MR = 25 – 3Q2 .
Problem 3. International Trade
Consider the market for ice skates in Iceber gland. Domestic demand and supply are given by the following equations:
P = 20 - (1/10)QD
and P = 2 + (1/20)QS
where P is the price of ice skates in dollars and Q is the quantity of ice skates in pairs.
(a) Suppose Icebergland is in autarky (that is, I cebergland is a closed economy). Find the equilibrium price and quantity in the market for ice skates. What are the values of producer and consumer surplus in the market for ice skates? Show your answers on a graph.
(b) Suppose the world price for ice skates is $4 pe r pair. Suppose that Icebergland opens its market for ice skates to world trade. How many pairs of ice skates do domestic firms produce and how many pairs do domestic c onsumers consume? How many pairs are exported or imported? What are the values of domestic consumer and producer surplus 3 in the ice skates market once this market is open to trade? Show your answers on a graph.
(c) Now suppose that the government of Icebergla nd imposes a tariff of $1 for each pair of ice skates that is importe d. Now how many pairs of ice skates are produced and consumed domestically? How many are importe d or exported? What are the consumer and producer surpluses, deadweight loss, and government revenue from the tariff? Show your answers on a graph.
(d) Suppose that instead of a tariff, the governme nt of Icebergland imposes an import quota of 60 pairs of ice skates. Now how many pair s of ice skates are produced and consumed domestically? How many are imported? What are the domestic producer and consumer surpluses, deadweight loss, and government re venue from the tariff? Show your answers on a graph.
Problem 4. Computing GDP
In Catan, to build a road you need 1 unit of wood and 1 unit of brick. All objects are valued in terms of ore. Their pr ices are given in the table below for the years 2011 and 2012.
Wood Brick Road
2011 1 ore 5 ore 10 ore
2012 1 ore 1 ore 4 ore
(a) Compute GDP in 2011 using the expenditure ap proach, then using the factor payments approach, and, lastly, the value-added approach.
(b) Compute GDP in 2012 using the expenditure ap proach, then using the factor payments approach, and, lastly, the value-added approach.
(c) What is the growth rate of nominal GDP from 2011 to 2012?
(d) Is there more output in Catan in the year 2011 or in 2012? Explain your answer in light of part (c).
Problem 5. Unemployment
(a) There are 150,000 citizens in Palmville who are age 16 and older. Of these citizens, 120,000 participate in the labor force and 90,000 are employed. What are Palmville’s unemployment and labor force participation rates?
(b) In Gnomesburg, labor supply and demand are given by the following equations:
W = 2 + 2QS
and W = 20 - QD
where W is the wage and Q is quantity of labor in thousands of workers. What minimum wage woul d give structural unemp loyment of 6,000 workers?
Problem 6. Price Indices and New Products People in a certain economy value two things: function and style. Products are bundles that give individuals different amounts of function and style. In years 1 and 2, there are two products which are creatively branded as product X and product Y. In year 3, a new product is created, product Z. The following table lists the prices of the goods in each of the three years, followed by how much function and style the good provides:
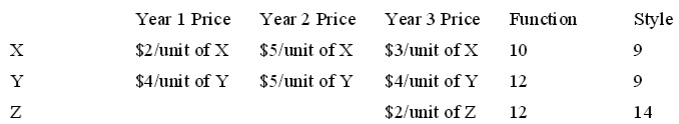
(a) If the market basket for this economy is origin ally 1 unit of X and 2 units of Y, what is the value, measured in dollars, of the market ba sket in year 1? What is the value of the same basket in year 2? If year 1 is defined to be the base year, what is the CPI in year 2 (the CPI in year 1 will be 100)? What is th e inflation rate between years 1 and 2? (Hint: You will not need the "function" and "s tyle" columns to find these answers.)
(b) A problem with using CPI to measure the "average " price is that it is defined in terms of goods. So, when a new product is introduced, it is difficult to decide how much of that product should be included in the "market basket" for the economy. For example, good Z above causes problems when trying to compute inflation between years 2 and 3. What if the BLS (Bureau of Labor Statistics) took th e following approach: in stead of tracking the change in price of the goods, they tracke d the change in pri ce of the different characteristics of the good? Say, instead, they defined the market basket as a certain 5 amount of function and style. What function an d style basket would be equivalent to the basket from part (a)?
(c) If you can only consume discrete (1,2,3...) amounts of each good, what is the least amount a consumer can spend to get at least th e function and style bask et in part (b) in the years 1, 2, and 3.
(d) Now, take the values computed in (c) as the value of the market basket in years 1, 2, and 3. Calculate the inflation rate between year s 1 and 2, and the rate between years 2 and 3.
(e) Did the inflation rate calculated in part (a) over or under-state infla tion from years 1 to 2 as measured in (d)? Calculate the CPI from years 2 to 3 by using the same market basket as in part (a) (2 units of Y and 1 unit of X) and the same base year (year 1). Does the inflation rate between years 2 to 3 calculated using the “goods”-based CPI over or understate the inflation rate calculated in part (d)?