1. Monopoly:
Because of a drug patent, the market for a certain new prescription drug is a monopoly. Assume the market demand is given by P = 130-2Q. The marginal cost is given by MC = 10 + Q.
a. What is the marginal revenue curve of this monopolist
b. Graph the demand, marginal revenue, and marginal cost curves.
c. What is the socially optimal level of production
d. What is the monopolist’s ideal quantity of production if the monopolist only charges one price for the good What price does he charge
e. What are the consumer and producer surpluses for the monopolist described in part (d) What is the deadweight loss for this monopolist Mark these areas on your graph.
f. If the total cost curve is given by TC = 15 + 10Q + Q2, what is the monopolist’s ATC What’s the monopolist’s profit In the LR, can the monopolist stay in business (Note: you do not need to graph TC or ATC to do this question.)
g. T/F: The “double-the-slope” method for finding MR works both when your demand curve is solved for Q and when it is solved for P.
2. Natural Monopoly:
Suppose a local utility company has a TC function given by TC = 400 + 4Q. The demand is given by P = 120 - 4Q, and the MC is constant at $4.
a. What’s the equation for the ATC
b. If the government decides to regulate the industry through MC pricing, what’s the minimum subsidy necessary to keep the firm in business
c. Suppose this firm is regulated and told that it must produce at least 15 units of the good and that it should select that price and output given its cost curves that will result in the firm earning zero economic profit. Given this regulatory directive, what price and quantity will be produced
3. Externalities:
On Aloha Island, the supply of widgets is given by P = 30-Q and the demand for widgets is given by P=Q. It is estimated that for every widget that’s produced, the factory creates enough pollution to cost the local fishing industry $2.
a. What is the market equilibrium without regulation
b. What is the e quation for the Marginal Social Cost curve Use this to figure out what the socially optimal amount of widgets is. Is the socially optimal the same amount as you found in part (a)
c. The government could achieve the out come in (b) by charging a “pollution tax” on each widget produced equal to $2. What would be the deadweight loss if the government did not do this (Hint: draw a graph with the unregulated market supply curve, the MSC, and the demand curve. Use your notes to identify the DWL on this graph.)
4. First Degree Price Discrimination:
Suppose the market demand for psychics is given by the equation: P = 105 - 2Q. Currently, there are many psychics in the market , and because there is so little cost to being a psychic, the market is perfectly competitive. The marginal cost of being a psychic is $5.
a. Graph the demand and marginal cost for the psychic market.
b. Calculate the equilibrium quantity of psychic consultations in this market.
c. What are the producer, consumer, and total surpluses Label the m on your graph.
Scientists have come out with a new test to determine with 100% accuracy whether or not someone is a psychic. After testing all of the psychics that practiced in the United States, they found that there was only one who was actually what she claimed to be. Now, the lone psychic Miss Cleo, is a monopolist psychic. Miss Cleo's marginal cost for providing her services is a constant $5.
Now that she is a monopolist, Miss Cleo decides to take advantage of her gif t and to practice first-degree price discrimination.
d. What is the equation for marginal revenue
e. On a separate graph from parts (a) and (b), graph the demand, marginal revenue, and marginal cost for Miss Cleo.
f. Calculate the equilibrium quantity of psychic consultations in this market.
g. What are the producer, consumer, and total surpluses Label the m on your graph.
h. What is the dead weight loss from Miss Cleo acting as a perfect price discriminating monopolist Give a conceptual explanation of why this is the case (i.e. using notions of efficiency).
5. Third Degree Price Discrimination:
Starplex Cinema is trying to decide whether or not to use third degree price discrimination. They think that the demand for movie tickets by college students is much more elastic than it is for their other patrons.
Starplex does some economic studies and finds that the demand for college students is given by P = 12 - QS. Starplex also finds that demand for movie tickets by non-college patrons is P = 20 - 2QA. Suppose that Starplex has a constant marginal cost of $3.
a. Graph the market for movie tickets on three graphs. One for the total movie ticket demand, one for n on-student demand, and one for student demand.
b. Calculate the aggregate demand curve.
c. Calculate the aggregate marginal revenue curve.
d. What total quantity of movie tickets will be sold by Starplex
e. What price would Starplex charge if it were a single price monopolist and not a price discriminating monopolist [Hint: this price is not a whole number, you might want to use your calculator here.]
f. Suppose that Starplex decides to implement third degree price discrimination. How many tickets will be purchased by college students What price should Starplex charge college students [Hint: carry your answer out to two places past the decimal.]
g. Suppose that Starplex decides to implement third degree price discrimination. How many tickets will be purchased by non-students What price should Starplex charge n on-students
6. Game Theory:
Suppose that that there are two musicians: Ricky Rock Star and Harry Hip Hop. Working by himself Ricky can capture the rock audience and earn a profit of $ 5 million. Working by himself Harry Hip Hop can capture the rap audience and earn a profit of $5 million. If the two musicians decide to collaborate they can also capture a third audience of listeners who like rap-rock fusion. Capturing this
audience is worth a total o $3 million in profit that the two musicians would need to split evenly.
Both musicians have two possible options: (1) he can collaborate with the other musician and share all three markets or (2) he can go it a lone and try to win over the other markets separately.
If a musician chooses not to collaborate, then he can release a CD much more quickly than if he worked with an other artist. Therefore, if one musician chooses to collaborate and the other does not, then the artist going it alone will be able to release a CD and earn all of their own market and the fusion audience. If both decide to work alone, then the fusion audience becomes disillusioned with the music industry and refuses to buy any records.
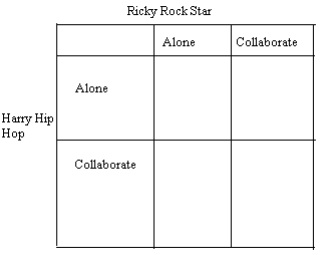
a. Construct a pay off matrix from the above information. The following matrix is provided for your convenience.
b. Is there a strictly dominant strategy for Ricky Rock Star
c. Is there a strictly dominant strategy for the Harry Hip Hop
d. What will be the outcome of the game
e. Is this outcome socially optimal (i.e. can no one be made better-off without making some one else worse-off) If so, why If not, which outcome is socially optimal