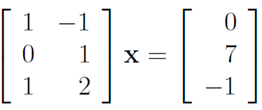Questions:
Linear Algebra: Vectors and Least Squares Problems
1. Consider the set of vectors:
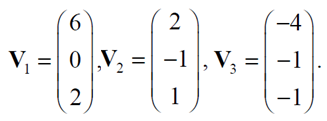
Do they form a basis in R^2? Give reasons.
What is the dimension of space spanned by these vectors?
2. Find the orthogonal projection of the vector u = (-2, 2, 3) onto the subspace spanned by vectors v1 = (3, -1, 0) and v2 = (1, -2, 1).
3. Given the vectors (4, 2, 1), (2, -1, 1) and (2, 3, 0)
(a) Determine whether these vectors are linearly independent or dependent.
(b) What is the dimension of the space spanned by these vectors?
4. Find the least squares solution to the equation: