Assignment:
The mass m1 moves on a smooth horizontal plane, m2 moves vertically under the force of gravity and the spring. Using polar coordinates r, theta for m1, l for m2 and taking b for the total length of the string plus the unstretched length of the spring, find:
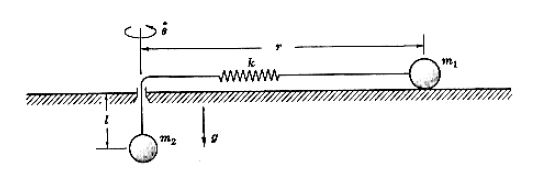
a. The Langrangian of the system
b. The equations of motion for mass m1 in terms of the radial coordinate r, and for m2 in terms of l
c. At any given angular velocity, theta, there will be 'equilibrium' values for the positions of m1 and m2. Find these values r zero and l zero.