Assignment:
Consider a bead of mass m sliding without friction on a wire that is bent in the shape of a parabola and is being spun with constant angular velocity ω about its vertical axis, as shown in figure.
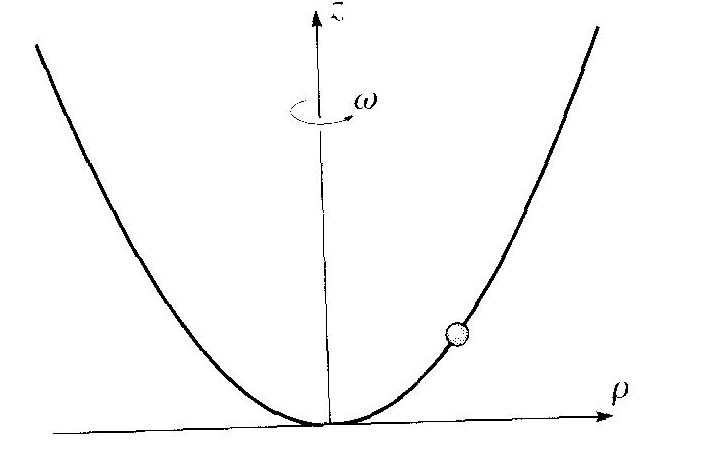
Use cylindrical polar coordinates and let the equation of the parabola be z=kΡ^2. Write down the Lagrangian in terms of Ρ as the generalized coordinate. Find the equation of motion of the bead and determine whether there are positions of equilibrium, that is, values of Ρ at which the bead can remain fixed, without sliding up or down the spinning wire. Discuss the stability of any equilibrium position you find.
Provide complete and step by step solution for the question, use formulas.