Assignment:
1. Consider the problem of a firm which has a production function described by:
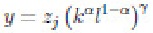
Suppose the firm is labor at constant wage rate lit and bugs units of capital at constant price Pk, respectively.
(a) Solve the maximization below and derive the expression for the operating profits of firm at time t, πt:
πt = maxlt{yt - Wlt}
Suppose the &in maximizes the present discounted valued of future dividends, dt = πt - Pkit, where in men vestt, it = kt+1 (1- δ)kt. Assume the discount factor for the firm, R, is constant, while its productivity zt follows an ARM process.
(b) Write down the maximization problem for the typical firm in recursive form.
Identify the endogenous and exogenous state variables for the problem.
(c) Derive the Euler equation and the envelope condition for the optimal choice of capital.
(d) Solve the problem and compute the (log of the) optimal choke of capital, kt+1.
(e) What is the elasticity of the optimal choice of capital with respect to gross interest rates, log(R).
2. Consider the problem. of a consumer that maximizes:
U = E0 [t-0Σ∞ βt ((a+Θt)ct - bc2t)]
s.t kt+1 + ct = kt/β + yt
where- the shock Θ captures taste Shocks to the marginal utility of consumption.
(a) Derive the first order conditions for this problem.
(b) Assuming Θt follows an AR(1) process with mum 0, characterize the process for optimal consumption.
(c) What is the process followed by consumption when Θt is a random walk?