Assignment:
1. The length of time to do a complete full service oil change at Speedy-Lube is normally distributed with a mean of 15.8 minutes and a standard deviation of 2.2 minutes
|
X
|
P(X < x)
|
P(X > x)
|
Mean
|
Std dev
|
|
11
|
.0146
|
.9854
|
15.8
|
2.2
|
|
15
|
.3581
|
.6419
|
15.8
|
2.2
|
|
21
|
.9910
|
.0090
|
15.8
|
2.2
|
|
24
|
.9999
|
.0001
|
15.8
|
2.2
|
|
|
p(lower)
|
p(upper)
|
|
|
(A) Analyze the output above to determine what percentage of complete full service oil changes will fall between 15 and 21 minutes.
(B) What percentage of complete full service oil changes will take less than 11 minutes? If 1000 cars had a complete full service oil change, how many would you expect to be finished in less than 11 minutes?
2. A random sample a 16 Google mangers yield the following information on annual salaries. The sample mean is $79,000, with a sample standard deviation of $6,000. What is the mean salary of all Google managers? What is the 95% confidence interval for the population mean?
Confidence interval - mean
|
95%
|
confidence level
|
|
79000
|
mean
|
|
6000
|
std. dev.
|
|
16
|
n
|
|
2.131
|
t (df = 15)
|
|
3197.174
|
half-width
|
|
82197.174
|
upper confidence limit
|
|
75802.826
|
lower confidence limit
|
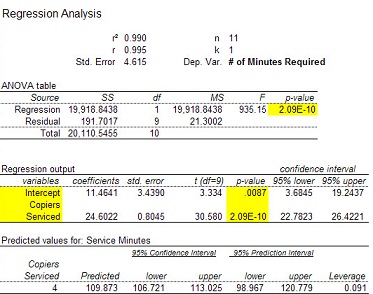
3. Accu-Copiers, Inc. sells and services the Accu-500 copying machine. As part of its standard service contract, the company agrees to perform routine service on this copier. To obtain information about the time it takes to perform routine service, Accu-Copiers has collected data for 11 service calls. The service calls information revealed the following:
Refer to the MegaStat output below to answer questions A through G.
(A) Analyze the above output to determine the regression equation.
(B) What conclusions are possible using the meaning of b0 (intercept) and b1 (regression coefficient) in this problem? (That is, explain the meaning of the coefficients.)
(C) What conclusions are possible using the coefficient of determination (r-squared)?
(D) Calculate the coefficient of correlation. Interpret this value.
(E) Does this data provide significant evidence (a=0.05) that the time to perform routine services is associated with the number of copiers serviced? Find the p-value and interpret.
(F) Predict the average number of minutes required to service four copiers.
(G) What is the 95% confidence interval for the number of minutes required for four copiers requiring service? What conclusion is possible using this interval?