How is this production function increasing returns to scale

Question

Assignment:

Questions

1. Given production function: Y = L^αK^β , α, β ∈ 0, 1, and determine

(a) how is this production function increasing returns to scale (IRS)? decreasing returns to scale (DRS) or constant returns to scale (CRS) with respect to L and K, based on the value of α and β. (You need to give your reasonings)

(b) derive marginal product of L and K. Is marginal product of labor increasing as labor increases? why?

(c) holding K constant now, and suppose α = 1. now the production function becomes Y = L · K¯, K¯ is fixed as a constant. Is the production function now IRS, DRS, or CRS? Why?

(d) suppose the labor market is competitive; we use w to represent a single worker's wage and p to represent the final product's price. Derive the wage equation for workers who work for under the above production technology.

2. Suppose, two sectors: Football vs. Soccer; two countries: US vs. Mexico; two factors: labor vs. capital. (standard 2× 2 × 2 HO model).

Now consider a single economy (U.S.), production functions for both sectors are as below:

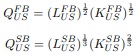
What is also nice about this example is that up until the last step (where we pin down the autarkic equilibrium relative price), the method will be identical for how you would solve for the free trade equilibrium.

(a) Under autarky, will the U.S. produce both goods? Why or why not? (You can answer this by using intuition or math, but first, draw a PPF graph)

(b) Write down the profit maximization problem for both sectors

(c) Solve the First-order conditions for both sectors with respect to both factors (aka the equilibrium wage and rental rate in each sector.)

(d) Draw the Wage-Rental ratio as a function of Labor-Capital ratio for both sectors (aka the factor intensity)

3. Consider a Heckscher-Ohlin model with two countries (the U.S. and Mexico), two goods (footballs and soccer balls), and two factors of production (high skilled labor H and low skilled labor L). Suppose that footballs/soccer balls are produced with production function:

Q_i^FB= (H_i^FB)^Φ . (L_i^FB) ^1-Φ

Q_i^SB = (H_i^SB)^σ (L_i^SB) ^1-σ

for i ∈ {US, MEX}, where φ > σ, suppose that L_US = L_MEX, H_US > H_MEX, and H_US and H_MEXare not "too" dissimilar.

(a) Draw the equilibrium production possibility frontier for the U.S. and Mexico. How do we see which good the U.S. imports? How do we see that equilibrium condition #2 (consumer optimization) holds? (Graphically show this)

(b) Suppose that the population of low skilled workers in Mexico doubles. Using words, figures, math or some combination thereof, show how this will affect the utility of high skilled workers, low skilled workers, and the overall welfare (i.e. the representative agent) in the United States.

(c) (bonus) If the population of low skilled workers in Mexico had halved instead of doubled, would your answer just be the opposite of what you said in part (b)? Why or why.`