Assignment:
Problems:
1. You drop a magnet through a loop of wire.
a. Sketch a plot of the magnetic field as a function of time through the loop.
b. Sketch a plot of the emf as a function of time in the loop.
The first part should be easy, just imagine dropping a magnet. The second part requires Faraday's law. Recall that the emf is the derivative of the magnetic flux with respect to time. This is mathematically similar to how velocity is the derivative of position with respect to time.
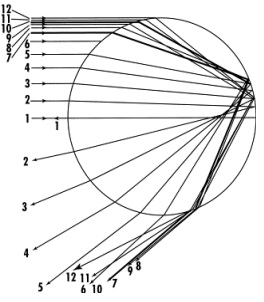
2. Assuming that raindrops are spherical can you show that a rainbow is located around 42o around a line from the sun to you (in other words, if you look at the shadow of your head on the floor the rainbow is a circle centered at this location but at an angle of 42oout).
Look at the rays that are traced through the spherical droplet in the diagram to the right. Note that they "bunch up" at a particular angle (rays 7-9 in the diagram). In other words, the angle of deviation (between the light coming in and the light reflecting back out) doesn't change much at the angle at which the rainbow is seen. Start by finding an expression for the angle of deviation as a function of incident angle. Next take its derivative with respect to the incident angle and put it equal to zero (wolfram alpha can handle this, or you can plot it instead). Then find the angle of deviation at which this occurs. This should be around 180o - 42o or 138o.
3. A thin layer of oil has a wonderful metallic rainbow color as it glistens of the surface of the Gulf of Mexica, having leaked from the Deepwater Horizon Oil Spill and been responsible for the death of the 8,332 species living in the region, including more than 1,200 fish, 200 birds, 1,400 mollusks, 1,500 crustaceans, 4 sea turtles and 29 marine mammals. If the thickness of the oil film is 1 m and the refractive index of the oil is 1.2, calculate the colors that appear the most brightest when viewing the oil film from above.
This is very similar to the problem in the notes at the end of cycle 1 (but with dead fish). Just remember to consider the phase shifts and the change in wavelength in the oil film.
4. Consider a system consisting of 3 charges. A 1 μC charge is located at x = 0, a 2 μC charge is located at x = 2 cm and -1 μC charge is located at x = 5 cm.
a. Obtain an expression and sketch a plot of electric potential as a function of x
b. Obtain an expression and sketch a plot of electric field as a function of x.
This is just a system of three point charges. The electric field and electric potential can be added together for the three charges to get the total electric field and electric potential for the entire system.
However, note that only one of the charges is located at the origin. Therefore, the r in the equations (distance from point charge) is going to have to be modified as you may be closer or further from thecharge depending on where it is located! Test your expressions. What if you are located at the same location as the charge? Does the term for this charge give you 0 for the distance away from the charge?
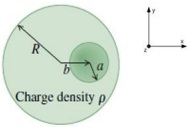
5. Imagine there is a charged sphere, where the charge is uniformly distributed over its volume. The electric field inside this sphere would ordinarily be given by Gauss' law because the sphere is spherically symmetric. However, what if we broke this symmetry? What if we introduced a spherical cavity inside the sphere which is off-center?
Find the electric field inside this spherical cavity.
This is really easy, once you figure it out! The only hint I'll give is that although it appears to be related to Gauss law, check out the section on superposition (adding stuff together) as it may help.
6. In the lecture we used the superposition principle to investigate the electric field along the axis of a uniformly charged ring. Could we use the same principle to find the electric field along a line perpendicular to the plane, and going through the center, of a uniformly charged square.
How does the square geometry affect the math?
Plot the electric field along the axis of a uniformly charged ring, and the electric field through the center of a uniformly charged square on the same plot.
This is similar to the problem in the notes, but here the integration may require wolfram alpha as the distance isn't constant anymore. However, due to symmetry we can still expect the electric field to be entirely in the x-direction. Furthermore, we don't necessarily have to integrate the entire square just a part of it as if we broke the square into 8 parts (each side broken in two) then each part would contribute equally to the electric field. Good luck!
7. You were asked to consider two atomic nuclei as if they were point charges of magnitude 1.6x10-19 C and mass of 1.66x10-27 kg. In particular you tried to determine how fast the nuclei would have to be traveling to get to within 1x10-15 m of each ther.
Can you do this in an easier way now?
Without using energy this is a much more challenging problem. However, now that you have been introduced to potential energy it should be very easy!
8. Consider a cell which has a 7.5 nm thick membrane and a membrane surface area of 5 x 10-9 m2 . The relative permittivity of the insulating cell membrane is 8.7 and the membrane has a resting potential of 60 mV.
Note that this electric potential arises due to the combination of ion pumps and ion channels in the cell membrane, which separate charge from the inside and outside of the membrane.
a. What is the magnitude of the charge on the inner and outer surfaces of the cell membrane?
b. How many ions does this charge correspond to?
The first part can be solved very easily by treating the cell membrane as a parallel-plate capacitor.
The second part is just converting the charge in coulombs to the number of ions (each with a charge of 1.6x10-19 C).
9. Imagine that in order to protect your house from building up positive charge and attracting a lightning strike you install a dissipative lightning rod. During a thunderstorm the corona discharge from your dissipative lightning rod into the surround air has a current of 1x10-4 A.
a. If the thunderstorm lasts for an hour, and the discharge is constant during this time, how much electric charge flows out of the lightning rod?
b. How many electrons flow into the lightning rod from the surrounding air?
From the definition of what current is you should be able to solve part a with no trouble. Similar to the last problem, you then have to write this charge in terms of the number of electrons (each with a charge of 1.6x10-19 C).