Assignment:
1) A person is running horizontally with a constant velocity v = 1.8m /sˆ i . A 2 m measuring stick is aligned parallel to the runner's motion and lies on the ground just to the side of the her path. The runner removes a quarter from her pocket which she then releases (lets go of) when the coin's horizontal position is aligned with the 0 cm mark on the stick. Her hand is 1.1 m above the ground at the point of release. You did an experiment like this in class.
a) Using a coordinate system whose origin is at the 0 m mark of the stick, whose x axis is the stick and whose y axis extends upwards perpendicular to the stick, write out position time equations, y(t) and x(t), for the motion of the quarter assuming it is released at t=0. Only y, x and t should be unknowns.
b) Use the equations from part a to determine the point along the measuring stick where the quarter first hits the ground. (Note: we are treating the quarter as a mass point, i.e. a particle.)
c) Determine the speed of the quarter just as it hits the floor. What angle does it's velocity vector make with the horizontal?
d) Imagine a coordinate system whose origin is at ground level but which moves with the runner. How should the equations from part a be modified so as to be consistent with this coordinate system? Explain your reasoning. It is in terms of this coordinate system that the runner views the motion of the quarter. Relative to this coordinate system, what is the speed of the quarter as it hits the floor and at what angle relative to the horizontal is the velocity vector directed?
2) If a satellite is orbiting Earth in a circle in the direction shown around the equator at an altitude of one Earth radii, the distance between it and the center of Earth is twice the radius of Earth. See Diagram. The local acceleration due to gravity at this altitude is one fourth the value at the surface of the planet (=9.8 m/s2 ).
a) At what speed is the satellite travelling?
b) Express the position, velocity and acceleration vectors of the satellite in unit vector notation1 at two points on the orbit: as it crosses the + x axis and as it crosses the -y axis.
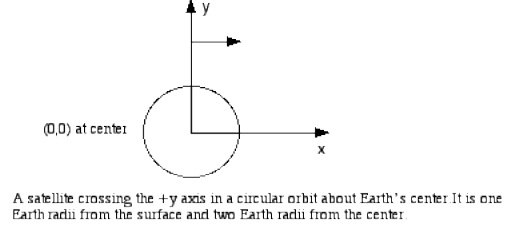
Using the given coordinate system.
For questions 3 and 4 see diagram below. These problems involve use of Newton's first law as well the kinematics we have already covered.
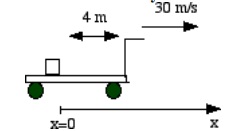
3) A large block of ice is on the floor of the bed of a flatbed truck and the truck is traveling at a constant speed of 30 m/s in a straight line. The truck then slows down to a speed of 5 m/s over a fairly short time interval. Imagine two observers, one in the bed of the truck and another on the ground who each track the motion of the ice block from their respective reference frames as the truck slows down. There is negligible friction between the ice block and the bed floor.
a) Describe the motion that each person observes. Be specific.
b) The observer in the truck bed claims that the block of ice has accelerated forward and therefore an unbalanced force acts on the block. The ground based observer disputes this claim and uses Newton's first law and the observations he made regarding the ice block's motion to support his argument. What might the ground based observer say, assuming he gets it right?
4) Imagine that at t=0 the block of ice on the floor of the same truck as in question 3 is at the rear of the truck bed 4 m from the front and both the truck and the block of ice are moving forward at 30 m/s. At this instant the driver steps on the brakes and the truck begins to slow down at 7 m/s2. The acceleration of the truck then remains constant until it stops. Recall that there is negligible friction between the ice and the bed floor.
a) If the ground based observer (from question 3) were to plot a position-time graph of the ice block's motion from t=0 until just before it hits the front of the cargo compartment, based on the coordinate system in the diagram2 , what would that graph look like? Make a careful sketch. Briefly explain why you sketched the graph as you did.
b) What is the slope of the graph you sketched in part a (the numerical value)? Explain your reasoning. How does the principle of inertia (Newton's first 1st law) apply to the motion of the ice? Briefly explain.
c) Write out separate position-time equations for the ice and the front of the truck bed referenced to the ground based observer's x axis (as above). Leave x and t as unknowns but specify all other values.
d) Use the equations in part c to determine the point in time when the ice collides with the front of the truck bed. How far has the ice moved relative to the ground based observer during this time interval? How far has the ice moved relative to the observer in the truck bed?