Discuss the below:
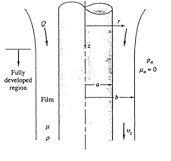
Q: Consider a viscous film of liquid draining uniformly down the side of a vertical rod of radius a, as in Fig. At some distance down the rod the film will approach a terminal or fully developed draining flow of constant outer radius b, with z =z(r)r = 0. Assume that the atmosphere offers no shear resistance to the film motion. Derive a differential equation for z, state the proper boundary conditions, and solve for the film velocity distribution. How does the film radius b relate to the total film volume flow rate Q?