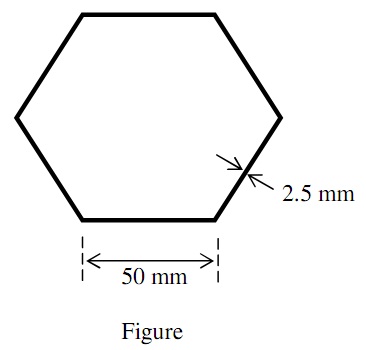
Q1. An aluminium alloy strut has the hollow regular hexagonal cross-section with side 50 mm each, and a constant thickness 2.5 mm all round along its length, see figure below.
The strut has both ends built-in and its material obeys the following stress-strain law in compression.
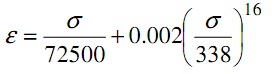
where the stress σ is in N/mm2
Determine the strut length that will carry the design load of 210 kN.
Q2. A material has a stress-strain relationship, which may be represented by the equation:
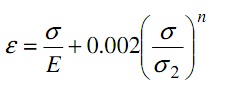
where ε = direct strain, and σ = direct stress
σ1 = 0.1% proof stress = 356 MPa
σ2 = 0.2% proof stress = 390 MPa
n = a constant
E = Young's Modulus = 70 GPa
A strut of thin-walled, tubular cross-section is made from this material, with a wall thickness of 2.5 mm, a mean diameter of 58 mm and an effective length of 700 mm, pinned about parallel diameters.
Using the tangent modulus method estimate the critical buckling load for this strut.