Problem 1. Give the slope and the y intercept of the following lines:
a. y = 2x+1
b. x - 1 = y
c. 3y + 2 = 5x
d. y = x
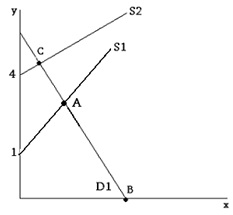
Problem 2. Use the figure above to answer the following questions:
a. If D1 is described by the equation y=5-2x, then what is the x-intercept of D1? Which point (A, B, or C) is it?
b. If S2 has a slope of 1, then what is the equation specifying S2?
c. If S1 has a slope of 2, then what is point A? (D1 is still as in part (a), also for the answer give the x and y coordinate.)
Problem 3. Countries Beta and Zeta each have 10 factories and can produce only sweaters or scarves. Output per factory is indicated in the following table:
Sweaters Scarves
Beta 10 100
Zeta 5 50
a. On separate graphs, graph the PPF for Beta and Zeta. Assume the PPF for both countries is linear with constant slopes. Also assume sweaters are the x variable and scarves are the y-variable.
b. What is the opportunity cost of a scarf in Beta? In Zeta?
c. What is the opportunity cost of a sweater in Beta? In Zeta?
Problem 4. You are given the following set of information. Find the slope and y-intercept, and the equation for each set of information.
a. (x,y) = (0,0) and (1,3)
b. (x,y) = (-4,1) and (5,3)
c. (x,y)=(3,2) and (4,2)
Problem 5. Suppose Sam is awake 16 hrs/day, and works 40hrs/week at his full time job. This job pays him $10/hr. Sam wants to buy a used car that costs $1800.
a. If Sam starts out with no money, how many weeks will he have to work before he can buy the car (assume he will by the car at the end of the week)?
b. Suppose Sam sees an ad soliciting some part time help for a mere $4/hr. If Sam works this job as well for 20hrs/week, then when can he buy the car?
c. Suppose again Sam has no money. Sam must also spend at least 50 hours a week taking care of his kids. What is the fastest (in number of days, now) that Sam can have enough money to buy the car?
Problem 6. Is the following statement positive or normative?
“There were more A’s in microeconomics last semester than D’s.”
If it’s positive, modify it slightly so that it becomes a normative statement. If it is normative, modify it slightly so that it becomes a positive statement.
Problem 7. (Harder) Consider the following figure. Assume the equation for D1 is y=5-2x. What would the slope of S1 have to be for point A to have a y-coordinate of 4?