Graph the function and indicate the relative extrema on

Question

1. f(x) = x³ -3/2x^2.

a) Find the (x,y) coordinates for the relative extrema.

b) Graph the function and indicate the relative extrema on your graph.

c) State the intervals where f(x) is increasing and where it is decreasing.

2.  f(x) = x⁴ + x³ - 3x² +1

a) Find the (x, y) coordinates of the point(s) of inflection.

b) Graph the function and indicate the point(s) of inflection on your graph.

c) On what interval(s) is f(x) concave up or concave down?

3. The linear price equation for a product is p=400-x. Sales increase from 149 to 150 units.

a) Find the change in revenue.

b) Use differentials to approximate the change in revenue.

4. A dairy farmer plans to enclose a rectangular pasture adjacent to a river. To provide enough grass for the herd, the pasture must contain 180, 000 square meters. No fencing is required along the river. What dimensions will use the least amount of fencing? Use the figure below to set up your objective function and constraint equation.

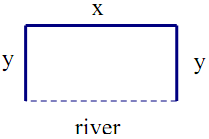
a) Define the objective function and the constraint equation.

b) What is the length of the shorter side and the length of the longer side of the rectangular plot?

5. f(x) = x² -1 /2x² -8

a) Find vertical asymptotes.

b) Find horizontal asymptote(s).

c) (2) Graph the function and indicate the asymptotes on your graph.

6. Using implicit differentiation, find dy/dx for the equation y³ + y² -5y -x² -4 and then evaluate the slope at (1, 1).

7. The price equation is p = 50/√x and the cost for x units is 0.5 500 C = 0.5x + 500.

a) Find the profit function.

b) Find the best price to maximize the profit.

8. An investment grows according to the model y = 1000e^0.066t.

a) What is the rate of change of the investment at time t?

b) Find the absolute maximum on the interval 0 ≤ 10 ≤ t.