Assignment:
Express the 2nd order ODE
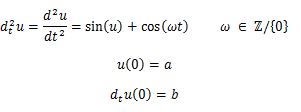
as a system of 1st order ODEs and verify that there exists a global solution by invoking the global existence and uniqueness Theorem.
Useful information:
Global existence and uniqueness Theorem:
The ordinary differential equation
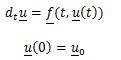
has a unique solution if
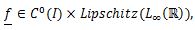
,f is continuous with respect to 1st variable and Lipschitz with respect to 2nd variable.
Lipschitz Continuity: A function g:I→R is Lipschitz continuous if ∃Λ>0 such that
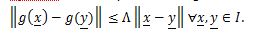
NB: means vector value.
Provide complete and step by step solution for the question and show calculations and use formulas.