Give a polynomial-time algorithm for this decision problem

Question

Problem 1:

Let G = (V, E,c,s,t) be a flow network with integer capacities, and f be a feasible flow with integer values. Suppose there is a edge e with head s and such that f(e) = 1. Describe an O(|V| + |E|) algorithm (An English explanation may be enough) that produces another feasible flow f' with |f|f'(e) = 0.

Be precise though: if you use an algorithm from the texbook, explain which graph is the input of the algorithm. Justify the overall running time and correctness.

Problem 2:

A multiple source-sink network is a tuple G = (V, E, c, S, T), where V is a set of vertices, E is a set of directed edges (parallel edges are allowed), S ⊂ V is the set of sources, and T ⊂ V is the set of sinks, c is a capacity function: c: E -> Z₊. Also, S ∩ T = 0. That is, sources are distinct from sinks.

A function f : E -> R₊ is called a flow if the following three conditions are satisfied:

1.  conservation of flow at interior vertices: for all vertices u not in S U T,

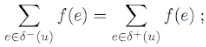
2.  capacity constraints: f ≤ c pointwise: i.e. for all e ∈  E,

f (e) ≤ c(e) .

Assume that non-negative quantities p_s, for s ∈ S, and q_t, for t ∈ T, ere given. The goal of this problem is to determine if a valid flow exists such that for all s ∈ S:

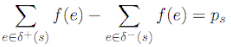
and such that for all t ∈ T:

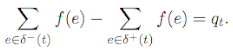
Use Network Flows to give a polynomial-time algorithm for this decision problem (the answer is YES or NO). Hint: read chapter 26.1 of the textbook.

Problem 3:

The edge connectivity of an undirected multigraph is the minimum number k of edges that must be removed to disconnect the graph. For example, the edge connectivity of a tree is 1, and the edge connectivity of a cyclic chain of vertices is 2. Show how to determine the edge connectivity of an undirected multigraph G = (V, E) by running a maximum-flow algorithm on at most |V| flow networks, each having O(|V|) vertices and O(|E|) edges.